Състав на графики

къдетоa1ikиa2kj–са елементи от матрицата за съседство на върховете съответно на първата и втората графика. Елементaijе равен на 1, ако в получената графикаG1(G2)има дъга, излизаща от върхаxiи влизаща вxj,и нула в противен случай.

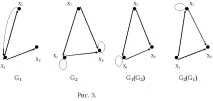
Пример.Извършете операцията по композиране за графиките, показани на фиг.11.3.

Нека съставим матриците на съседство на върховете на графа:

Изчислявайки елементите на матрицата съгласно (1), получаваме:

Декартово произведение на графики.

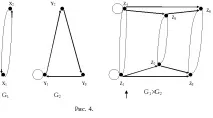
Нека дефинираме набора от дъги на резултантния график. За целта избираме групи от върхове на множествотоZ,, чиито компоненти съвпадат. В разглеждания пример има пет такива групи: две групи със съвпадащи компоненти от множествотоXи три групи със съвпадащи компоненти отY. Помислете за група от върхове в резултантната графа, които имат общ компонентx1:z1=(x1y1), z2=(x1y1), z3=(x1y3).Съгласно дефиницията на операцията на декартовото произведение на графите, множеството от дъги между тези върхове се определя от връзките между върховете на множествотоY. Така дъгата(y1,y1)в графикатаG2определя присъствието на дъгата(z1,z1)в резултантната графика. За удобство при разглеждането на всички дъги на получената графа ще направим таблица, първата колона на която изброява върховете със съвпадащи компоненти, втората колона изброява дъгите между несъвпадащи компоненти, а третата и четвъртата колона изброяват дъгите в резултантната графа.

---