Теорема на Щайнер – Инерционен момент

Теорема на Щайнер. Момент на инерция. Твърдение и доказателство на теоремата

Уважаеми посетители на сайта Училищен портал, предлага на вашето внимание работа по математика на тема„Теорема на Щайнер. Инерционен момент”, който представя материали от теоретичен и практически характер, препоръки за решаване на задачи с помощта на тази теорема.

Якоб Щайнер (1796-1863) е един от великите математици, който се счита за основател както на синтетичната геометрия на кривите линии, така и на повърхностите от втори и по-висок ред.

Що се отнася до Кристиан Хюйгенс, неговият принос в различни науки също не е малък. Той значително подобрява телескопа (до 92 пъти увеличение на изображението), открива пръстените на Сатурн и неговия спътник Титан, а през 1673 г. в доста информативната си работа „Часовник с махало“ представя работа върху кинематиката на ускореното движение.

Теорема на Щайнер – формулировка

Съгласно теоремата на Щайнер е установено, чеинерционният момент на тяло, когато се изчисли спрямо произволна ос, съответства на сумата от инерционния момент на тялото около такава ос, която минава през центъра на масата и е успоредна на тази ос, както и плюс произведението на квадрата на разстоянието между осите и масата на тялото, съгласно следната формула (1):

J=J0 +md 2(1)

Където във формулата приемаме съответно следните стойности:d - разстоянието между осите ОО1║О'O1';J0– инерционният момент на тялото, изчислен спрямо оста, която минава през центъра на масата и ще се определя от съотношението (2):

J0 =Jd =mR 2 /2(2)

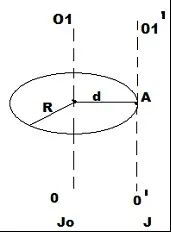
Тъй като d \u003d R, тогава инерционният момент около оста, която минава през определенатана фигурата точка А ще се определи по формула (3):

J =mR 2 +mR 2 /2 = 3 /2 mR 2(3)

Част 1. Динамика на въртене на твърдо тяло 1.1. Инерционни моменти на топката и диска 1.2. Теорема на Хюйгенс-Щайнер 1.3. Динамика на въртеливото движение на твърдо тяло — теоретични основи• Момент на импулса• Момент на сила• Инерционен момент спрямо оста на въртене• Основният закон на динамиката на въртеливото движение на твърдо тяло спрямо неподвижна ос

Част 2. Препоръки за решаване на различни типични проблеми

Част 3. Решаване на задачи за определяне на инерционния момент 3.1. Класически примери за решаване на проблеми 3.2. Намиране на инерционния момент на диска и топката• Задачи за определяне на инерционния момент на диска• Задачи за определяне на инерционния момент на топката Заключение Литература

Вижте презентацията„Теоремата на Щайнер. Инерционният момент" може да бъде по-нисък ↓

---