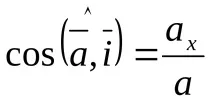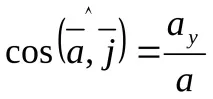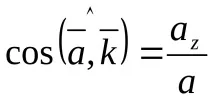Теоретична механика
за бакалаври ЗиДО
Съставител: д-р на техническите науки, проф. Смелягин А.И.
д.ф.н., ст.н.с. Kegeles V.L.
1 Кинематика. Общи понятия 2
2 Точкова кинематика 2
3 Кинематика на твърдо тяло 7
3.1 Постъпателно движение на твърдо тяло 7
3.2 Въртене на твърдо тяло около неподвижна ос 7
3.3 Равнопаралелно (плоско) движение на твърдо тяло 9
3.4 Сферично движение 15
4 Сложно движение на точки 17
1 Кинематика. Общи понятия
Кинематиката е дял от теоретичната механика, който изучава движението на материалните тела, без да отчита причините, които предизвикват това движение.
В класическата механика движението на материалните тела се разглежда в триизмерното евклидово пространство, а времето се счита за абсолютно, независимо от референтната система.
Референтна система - координатна система, неизменно свързана с тялото, по отношение на която се разглежда движението на изследваните обекти.
Ако отправната система е в покой, тогава движението на обект спрямо нея се нарича абсолютно. Движението на обект по отношение на движеща се референтна система се нарича относително.
Методите на кинематиката позволяват да се определи позицията на изследвания обект в разглежданата референтна рамка, както и да се намери неговата скорост и ускорение по всяко време.
Изучаването на раздела започва с кинематиката на точка (изолирана, принадлежаща на твърдо тяло или непрекъсната среда), след което се разглежда движението на твърди тела и техните системи.
2-точкова кинематика
Характеристиките на движението на точка във всеки един момент са нейното положение, скорост и ускорение.
Географското място на последователни позиции на точка се нарича траектория.
Да се определят характеристиките на движението и траекториятаточки обикновено използват три начина за уточняване на своето движение - вектор, координата, естествено.
Векторен начин за дефиниране на движение
P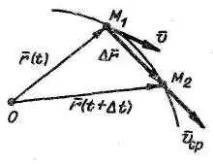
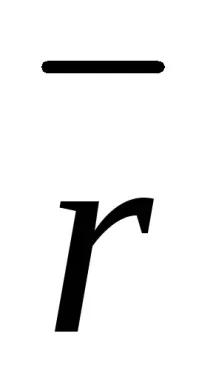
Уравнение на движение:
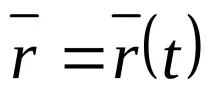
Траекториятана точката е ходографът на вектора
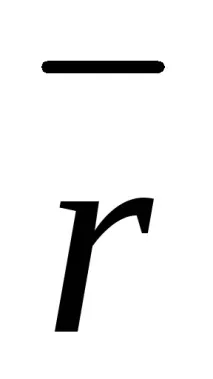
Средна скорост на точката във времето Δt
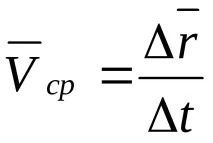
Скоростточки в момент t
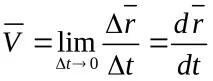
Векторът на скоростта B
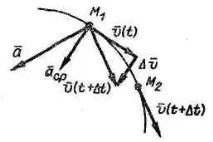
Средно ускорение на точката във времето Δt
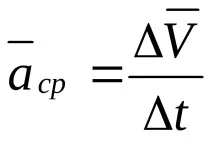
Точка наускорениев момент t
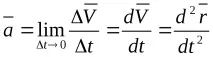
Този метод се използва като правило при теоретичния анализ на законите на движението.
И така,
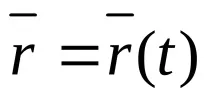
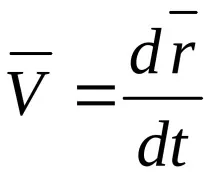
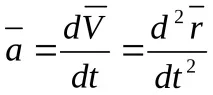
Координатен метод за определяне на движението
За описание на движението на точка се използват координатни системи: декартова, полярна, цилиндрична, сферична и др.
Позициятана точка в декартовата координатна система по всяко време се определя от нейните координати x, y, z.
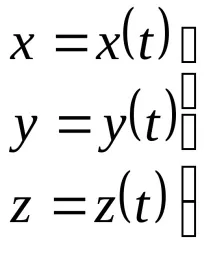
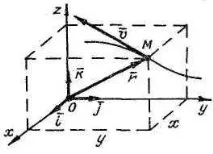
Тези уравнения определят траекторията на точка в параметрична форма.
Уравненията на траекторията на точката в координатна форма могат да бъдат получени чрез
изключвайки параметъра t от уравненията на движението, под формата на система от уравнения
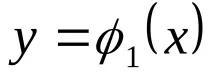
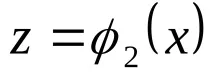
Скорост.
Така че
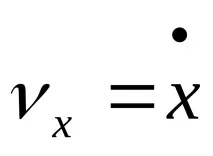
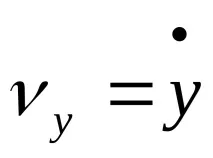
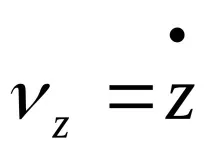
Скоростен модул
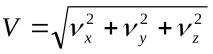
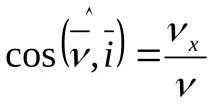
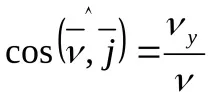
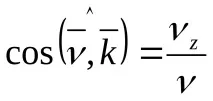
Ускорение,
след това
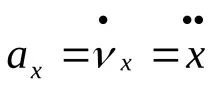
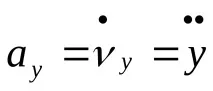
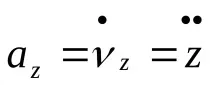
Модул за ускоряване
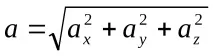
Насочващи косинуси