1. Селективен метод.
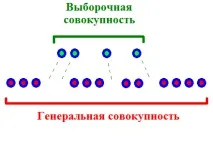
При изучаването на различни явления за оценка на голям брой наблюдения, в много случаи, когато се събира необходимата информация, методът на вземане на проби се използва широко. Същността на този метод се състои в това, че за да се оцени целия набор от наблюдения, необходимата информация се събира от определен брой наблюдения от този набор. Тези. изследваните наблюдения не включват целия набор от наблюдения, а само определен брой от тях. Цялата съвкупност от наблюдения се нарича популация. И всички наблюдения, избрани за проучването, са извадени. Методът, при който се използват всички обекти на изследваното явление, се нарича непрекъснат. Ако се изследва определен брой обекти от цялата популация, тогава този метод се нарича селективен (фиг. 1).
Предимствата на пробовземния метод пред непрекъснатия метод са съвсем очевидни. Първо, този метод може значително да намали цената на всички видове ресурси. На второ място, избраните за изследване обекти могат да бъдат изследвани много задълбочено, т.е. по много начини. Трето, в много случаи просто няма друга възможност за изследване на съвкупността от обекти.
Един от недостатъците, които възникват при използване на метод на извадка, е грешката в представителността. Тази грешка възниква поради факта, че не се изследва цялата популация, а извадка.
Фиг.1 |
Критерият, който трябва да се спазва при избора на обекти за изследване, е случайността. С други думи, всички обекти, избрани за изследването, трябва да бъдат включени на случаен принцип в извадката. В противен случай резултатите може да са неверни.
За избора на обекти, които ще бъдат подложени на изследване, обикновено се използва един от двата метода на вземане на проби. Първият метод включва връщане на обекта на изследване на общата съвкупност след неговото изследване. Вторият метод предвижда, че избраният обект няма да бъде върнат в общата популация след изследването му.
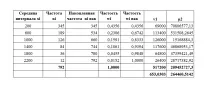
Числените характеристики на извадката се наричат съответно извадка. Основни характеристики:
Основната задача на извадковия метод на наблюдения е да се оценят характеристиките на генералната съвкупност от обекти на изследване според данните на извадката.
2. Оценка на параметрите на извадката.
Нека е даден общият набор от обекти на изследване. Броят на обектите в генералната съвкупност е N. Числото N е от голямо значение и не е възможно да се изследва цялата съвкупност. Поради тази причина се изследва извадката. И параметърът , който се изчислява за тази съвкупност, е оценка на параметъра θ на генералната съвкупност. От това можем да дадем следната дефиниция: оценката на параметъра на генералната съвкупност е стойността или функцията, изчислена от стойностите на случайната променлива X на извадката. Тези.
Например, нека параметърът θ е математическото очакване на случайна променлива X. Тогава оценката на този параметър ще бъде извадкатасредноаритметично.
Свойства на оценките. Основните свойства на оценките са безпристрастност, последователност и ефективност.
Безпристрастната оценка означава нейното отклонение от същия параметър на генералната съвкупност, т.е. математическото очакване на тази оценка е равно на оценения параметър.
Ако това равенство не е изпълнено, тогава получената оценка е надценена или подценена.
Съгласуваност означава приближаване на оценката до оценения параметър, когато n клони към безкрайност. Или сближаване на вероятността с параметъра на населението.
От това можем да заключим, че колкото по-голяма е извадката n, толкова по-точен е изчисленият параметър.
Ефективна оценка на параметъра θ е такава безпристрастна оценка, която има най-малката дисперсия от всички възможни безпристрастни оценки на параметъра θ и изчислена от извадка със същия размер n. Ефективността на оценката се изчислява от съотношението:
3. Вероятност за доверие. Пределна извадкова грешка.
Оценката на извадковата популация дава приблизителна стойност на оценения параметър, т.е. някаква точкова характеристика. За да получите по-широка представа за оценката на неизвестен параметър на популацията (не само точност, но и надеждност), се използва интервална оценка на параметъра θ. Интервалната оценка на параметъра θ се нарича интервалът, който покрива параметъра θ с дадена вероятност. Този интервал се нарича доверителен интервал, а вероятността γ се нарича доверителна вероятност или надеждност. Стойността на доверителния интервал силно зависи от дадената доверителна вероятност γ и от размера на извадката n.
Когато изучавате извадкова популация, изчислената средна аритметична стойност може да има някоиотклонение от средноаритметичното на генералната съвкупност. Това отклонение се нарича грешка на представителността, която възниква поради изследването не на цялата, а на извадката. Най-голямото отклонение на средната стойност на извадката от средноаритметичната стойност на съвкупността, което е възможно за дадено ниво на достоверност, се нарича пределна грешка на извадката.
Изграждане на доверителен интервал за генералната средна върху голяма извадка.
Доверителният интервал за общото средно с n от порядъка на няколкостотин се изчислява по следната формула:
γ - доверителна вероятност, изразена чрез функцията на Лаплас Ф(t).
променлива t е:
От това следва, че за дадена доверителна вероятност γ пределната грешка на средната стойност на извадката е равна на произведението от t (стойността на функцията на Лаплас) и стандартната грешка.
Доверителният интервал на общата средна стойност се изчислява по формулата:
За да се намери пределната грешка Δ, е необходимо да се намери средната квадратична грешка. Средната квадратична грешка се изчислява по следната формула:
При достатъчно голям размер на извадката n дисперсията на извадката се доближава до общата дисперсия, така че колкото по-голямо е n, толкова по-точна е стойността на средната квадратична грешка.
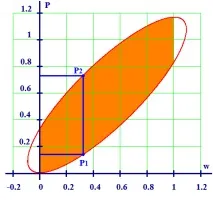
Построяване на доверителен интервал за генералната фракция за голяма извадка.
Ако разпределението на извадковия дял w се счита за приблизително нормално, тогава, за да намерим доверителния интервал за общия дял, използваме формулата за пределна грешка:
От тук получаваме границите на доверителния интервал p 1 и p 2 .
Фиг.2 |