Топлинна мощност на идеален газ

Ако в резултат на топлообмен на тялото се предаде определено количество топлина, тогава вътрешната енергия на тялото и неговата температура се променят. Количеството топлина Q, необходимо за нагряване на 1 kg вещество с 1 K, се нарича специфична топлина на веществото c.

c = Q / (mΔT).

В много случаи е удобно да се използва моларният топлинен капацитет C:

C = M c,

където М е моларната маса на веществото.

Определеният по този начин топлинен капацитет не е еднозначна характеристика на дадено вещество. Според първия закон на термодинамиката промяната във вътрешната енергия на тялото зависи не само от количеството получена топлина, но и от работата, извършена от тялото. В зависимост от условията, при които се извършва процесът на пренос на топлина, тялото може да извършва различни дейности. Следователно едно и също количество топлина, предадено на тялото, може да причини различни промени във вътрешната му енергия и, следователно, температурата.

Такава неяснота при определяне на топлинния капацитет е характерна само за газообразно вещество. При нагряване на течни и твърди тела техният обем практически не се променя и работата на разширението се оказва равна на нула. Следователно цялото количество топлина, получено от тялото, отива за промяна на вътрешната му енергия. За разлика от течностите и твърдите вещества, газът в процеса на пренос на топлина може значително да промени обема си и да извърши работа. Следователно топлинният капацитет на газообразното вещество зависи от характера на термодинамичния процес. Обикновено се разглеждат две стойности на топлинния капацитет на газовете: CV е моларният топлинен капацитет визохоричен процес (V = const) и Cp е моларният топлинен капацитет в изобарния процес (p = const).

В процеса при постоянен обем газът не работи: A \u003d 0. От първия закон на термодинамиката за 1 мол газ следва

QV = CV ∆T = ∆U.

Промяната ΔU на вътрешната енергия на газ е правопропорционална на промяната ΔT на неговата температура.

За процес при постоянно налягане първият закон на термодинамиката дава:

Qp = ΔU + p (V2 – V1) = CV ΔT + pΔV,

където ΔV е промяната в обема на 1 мол идеален газ, когато температурата му се промени с ΔT. Това предполага:

Съотношението ΔV / ΔT може да се намери от уравнението на състоянието на идеалния газ, написано за 1 мол:

pV=RT,

където R е универсалната газова константа. За p = const

или

По този начин връзката, изразяваща връзката между моларните топлинни мощности Cp и CV има формата (формула на Майер):

Cp = CV + R.

Моларният топлинен капацитет Cp на газ при процес с постоянно налягане винаги е по-голям от моларния топлинен капацитет CV при процес с постоянен обем (Фигура 3.10.1).

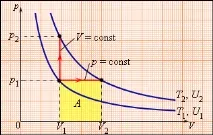Фигура 3.10.1. Два възможни процеса на нагряване на газ чрез ΔT = T2 – T1. При p = const газът извършва работа A = p1(V2 – V1). Следователно Cp > CV

Съотношението на топлинните мощности при процеси с постоянно налягане и постоянен обем играе важна роля в термодинамиката. Означава се с гръцката буква γ.

По-специално, това съотношение е включено във формулата за адиабатен процес (виж §3.9).

Между две изотерми с температури T1 и T2 на (p, V) диаграмата са възможни различни преходни пътища. Тъй като за всички такива преходи промяната в температурата ΔT = T2 – T1 е една и съща, следователно промяната ΔU на вътрешната енергия е една и съща. Работата A, извършена в този случай, и количеството топлина Q, получено в резултат на преноса на топлина, ще бъдат различни за различните преходни пътища. От това следва, че един газ има безкраен брой топлинни мощности. Cp и CV са само частични (и много важни за газовата теория) стойности на топлинните мощности.

Модел. Топлинни мощности на идеален газ

Термодинамичните процеси, при които топлинният капацитет на газа остава непроменен, се наричат политропни. Всички изопроцеси са политропни. В случай на изотермичен процес ΔT = 0, така че CT = ∞. При адиабатен процес ΔQ = 0, следователно Cad = 0.

Трябва да се отбележи, че "топлинен капацитет", както и "количество топлина" са изключително неудачни термини. Те са наследени от съвременната наука от теорията за калориите, преобладаваща през 18 век. Тази теория разглежда топлината като специална безтегловна субстанция, съдържаща се в телата. Смятало се, че не може нито да бъде създадено, нито унищожено. Нагряването на телата се обяснявало с увеличаване, а охлаждането - с намаляване на съдържащата се в тях калория. Калорийната теория е несъстоятелна. Не може да се обясни защо същата промяна във вътрешната енергия на едно тяло може да се получи чрез предаване на различно количество топлина в зависимост от извършената от тялото работа. Следователно твърдението, че "дадено тяло съдържа такъв и такъв запас от топлина", е лишено от физически смисъл.

В молекулярно-кинетичната теория се установява следната връзка между средната кинетична енергиятранслационно движение на молекули и абсолютна температура T:

Вътрешната енергия на 1 мол идеален газ е равна на произведението на числото на Авогадро NA:

Когато температурата се промени с ΔT, вътрешната енергия се променя с количеството

Коефициентът на пропорционалност между ΔU и ΔT е равен на топлинния капацитет CV при постоянно налягане:

Тази връзка е добре потвърдена в експерименти с газове, състоящи се от едноатомни молекули (хелий, неон, аргон). Въпреки това, за двуатомни (водород, азот) и многоатомни (въглероден диоксид) газове това съотношение не е в съответствие с експерименталните данни. Причината за това несъответствие е, че за дву- и многоатомните молекули средната кинетична енергия трябва да включва енергията не само на транслационното, но и на въртеливото движение на молекулите.

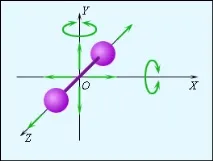Фигура 3.10.2. Модел на двуатомна молекула. Точка O съвпада с центъра на масата на молекулата

На фиг. 3.10.2 показва модел на двуатомна молекула. Една молекула може да извърши пет независими движения: три транслационни движения по осите X, Y, Z и две завъртания около осите X и Y. Опитът показва, че въртенето около оста Z, върху която лежат центровете на двата атома, може да бъде инициирано само при много високи температури. При обикновени температури въртене около оста Z не се случва, точно както едноатомната молекула не се върти. Всяко независимо движение се нарича степен на свобода. Така едноатомната молекула има 3 транслационни степени на свобода, "твърдата" двуатомна молекула има 5 степени (3 транслационни и 2 ротационни) имногоатомна молекула - 6 степени на свобода (3 транслационни и 3 ротационни).

В класическата статистическа физика се доказва така наречената теорема за равномерното разпределение на енергията по степени на свобода:

Ако системата от молекули е в термично равновесие при температура T, тогава средната кинетична енергия е равномерно разпределена между всички степени на свобода и за всяка степен на свобода на молекулата е равна на

От тази теорема следва, че моларните топлинни мощности Cp и CV на газа и тяхното съотношение γ могат да бъдат записани като

където i е броят на степените на свобода на газа.

За газ, състоящ се от едноатомни молекули (i = 3)

За газ, състоящ се от двуатомни молекули (i = 5)

За газ, състоящ се от многоатомни молекули (i = 6)

Експериментално измерените топлинни мощности на много газове при нормални условия са в добро съответствие с горните изрази. Като цяло обаче класическата теория за топлинния капацитет на газовете не може да се счита за напълно задоволителна. Има много примери за значителни несъответствия между теория и експеримент. Това се обяснява с факта, че класическата теория не е в състояние напълно да отчете енергията, свързана с вътрешните движения в молекулата.

Теоремата за равномерното разпределение на енергията по степени на свобода може да се приложи и към топлинното движение на частиците в твърдо тяло. Атомите, които изграждат кристалната решетка, вибрират около равновесните позиции. Енергията на тези вибрации е вътрешната енергия на твърдото тяло. Всеки атом в кристалрешетката може да се колебае в три взаимно перпендикулярни посоки. Следователно всеки атом има 3 вибрационни степени на свобода. При хармоничните вибрации средната кинетична енергия е равна на средната потенциална енергия. Следователно, в съответствие с теоремата за равномерното разпределение, всяка вибрационна степен на свобода има средна енергия kT и 3kT на атом. Вътрешната енергия на 1 мол твърдо вещество е:

U = 3NAkT = 3RT.

Следователно моларният топлинен капацитет на вещество в твърдо състояние е равен на:

C \u003d 3R \u003d 25,12 J / mol K.

Тази зависимост се нарича закон на Дюлонг-Пети. За твърдите тела практически няма разлика между Cp и CV поради незначителната работа, извършена при разширяване или свиване.

Опитът показва, че за много твърди вещества (химични елементи) моларният топлинен капацитет при обикновени температури наистина е близо до 3R. Въпреки това, при ниски температури има значителни несъответствия между теорията и експеримента. Това показва, че хипотезата за равномерно разпределение на енергията по степени на свобода е приближение. Експериментално наблюдаваната зависимост на топлинния капацитет от температурата може да се обясни само въз основа на квантовите концепции.

Не намерихте това, което търсихте? Използвайте търсачката: