Тригонометрични теореми

II основна част. 8

Общи сведения за тригонометричните функции. 8

Теорема за площта на триъгълника. 13

Синусова теорема. 14

Косинусова теорема. 16

III Заключение. 20

Библиография. 21

Въведение

Геометрията е една от най-древните и интересни науки, която се занимава с изучаването на геометричните форми. Нашият свят не може да си представим без тяхното съществуване. Тази наука има огромен запас от различни теореми, които постоянно се използват както при решаването на математически проблеми, така и в живота. Най-много ме интересуваха синусовите и косинусовите теореми, които се използват при решаване на произволни триъгълници. Целта на това есе е да можете да докажете теоремите за косинусите и синусите, да ги приложите при решаването на проблеми, да изберете правилния курс на решение, когато ги използвате, да знаете къде тези теореми се прилагат в живота.

триъгълници

Триъгълнике фигура, която се състои от три точки, които не лежат на една права линия, и три сегмента, свързващи тези точки по двойки. Точките се наричат върховена триъгълника, а отсечките са неговистрани.

Триъгълникът еравнобедрен, ако двете му страни са равни. Тези равни страни се наричат страни, а третата страна се наричаоснована триъгълника.

Триъгълник с равни страни се наричаравностраненилиправилен.

Триъгълникът се наричаостроъгълен, ако и трите му ъгъла са остри, т.е. по-малки от 90°
Триъгълникът се наричатъп,ако един от ъглите му е тъп, т.е. по-голям от 90°.

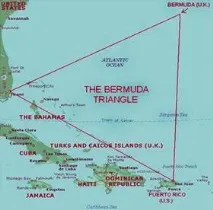
БермудитеТриъгълнике добре позната аномална зона. Намира се на границите между Бермудите, Маями във Флорида и Пуерто Рико. Площта на Бермудския триъгълник е над един милион квадратни километра. Релефът на дъното в тази акватория е добре проучен. На шелфа, който съставлява значителна част от това дъно, са извършени много сондажи за намиране на нефт и други минерали. Курсът, температурата на водата през различни периоди от годината, нейната соленост и движението на въздушните маси над океана - всички тези природни данни са изброени във всички специални каталози. Тази област не се различава особено от други подобни географски местоположения. И все пак именно в района на Бермудския триъгълник мистериозно изчезнаха кораби, а след това и самолети.

Излагат се различни хипотези, за да се обяснят тези изчезвания, от необичайни метеорологични явления до извънземни отвличания. Скептиците обаче твърдят, че изчезването на кораби в Бермудския триъгълник се случва не по-често, отколкото в други райони на световния океан и се дължи на естествени причини.Морето и самолетите умират в други части на земното кълбо, понякога безследно. Неизправност на радиото или внезапно възникване на бедствие може да попречи на екипажа да предаде сигнал за помощ. Търсенето на отломки в морето не е лесна задача, особено при буря или когато точното място на катастрофата е неизвестно. Като се има предвид много интензивният трафик в Бермудския триъгълник, честите циклони и бури, голям брой плитчини, броят на бедствията, случили се тук, които не са обяснени, не е необичайно голям.

Характеристика на такъв триъгълник, известен още от древността, е, че при такова съотношение на страните Питагоровата теорема дава цели квадрати както на краката, така и на хипотенузата, т.е. 9:16:25.Египетският триъгълник е най-простият (и първият известен) от триъгълниците на Херон - триъгълници с цели страни и площи.

Името на триъгълника с такова съотношение на страните е дадено от елините: през 7 - 5 век пр.н.е. д. Гръцки философи и общественици активно посещават Египет. Така например Питагор през 535 г. пр.н.е. д. по настояване на Талес той отиде в Египет, за да учи астрономия и математика - и, очевидно, това беше опит да се обобщи съотношението на квадратите, характерни за египетския триъгълник, към всеки правоъгълен триъгълник, който накара Питагор да докаже известната теорема.

Египетският триъгълник със съотношение на страните 3:4:5 се използва активно за изграждане на прави ъгли от геодезисти и архитекти.

За да се изгради прав ъгъл, се използва шнур или въже, разделен с маркировки (възли) на 12 (3 + 4 + 5) части: триъгълник, изграден чрез опъване на такъв шнур, се оказа правоъгълен с много висока точност, а самите шнурове бяха водачи за полагане на правилния ъгъл на конструкцията.

II основна част

Общи сведения за тригонометричните функции

Тригонометрияе гръцка дума и буквално означава измерване на триъгълници.

В този случай измерването на триъгълници трябва да се разбира като решение на триъгълници, т.е. определяне на страни, ъгли и други елементи на триъгълник, ако някои от тях са дадени. Голям брой практически задачи, както и проблеми на планиметрията, стереометрията, астрономията и други, се свеждат до проблема за решаване на триъгълници.

Появата на тригонометрията се свързва с геодезията, астрономията и строителството. Въпреки че името на науката възникна сравнително наскоро, много от понятията и фактите, които сега са свързани с тригонометрията, бяха известни с още двепреди хиляди години.

Концепцията засинусима дълга история. Всъщност различни съотношения на сегменти от триъгълник и окръжност (и по същество тригонометрични функции) се срещат още през 3 век пр.н.е. в трудовете на великите математици на древна Гърция - Евклид, Архимед, Аполоний от Перга. В римския период тези отношения са изследвани доста систематично от Менелай (1 в. сл. н. е.), въпреки че не са придобили специално име. Съвременният синус а, например, се изучава като полухорда, поддържана от централен ъгъл с големина а, или като хорда на удвоена дъга. През 4-5 век се появява специален термин в трудовете по астрономия на великия индийски учен Арябхата, на когото е кръстен първият индийски спътник на Земята. Той нарекъл сегмента AM ardhajiva (ardha - половина, jiva - тетива, която прилича на хорда). По-късно се появява по-краткото име джива. Арабските математици през 9-ти век заменят тази дума с арабската дума jayb (издутина). При превода на арабски математически текстове през века той е заменен с латински синус (синус - завой, кривина).

Думатакосинусе много по-млада.Косинусе съкращение на латинския израз completesinus, т.е. „допълнителен синус“ (или по друг начин „синус на допълнителна дъга“; cosa = sin(90° - a)).Допирателнитевъзникват във връзка с решаването на проблема за определяне на дължината на сянката. Тангенсът (а също и котангенсът) е въведен през 10 век от арабския математик Абул-Вафа, който съставя и първите таблици за намиране на тангенси и котангенси. Тези открития обаче остават неизвестни за европейските учени дълго време и тангентите са преоткрити едва през 14 век от немския математик, астроном Регимонтан (1467 г.). Той доказа теоремата за допирателната. Региомонтан също съставя подробна тригонометриямаси; Благодарение на работата му равнинната и сферичната тригонометрия стават самостоятелна дисциплина и в Европа.