Улеи за смет - изработка и монтаж
10.1. Класификация на сигналите
10.1.1. Класификация на измервателните сигнали
Сигнале материален носител на информация, който е определен физически процес, един от параметрите на който е функционално свързан с измерваната физическа величина. Такъв параметър се наричаинформативен.
Измервателен сигнале сигнал, съдържащ количествена информация за измерваната физична величина. Основните понятия, термини и определения в областта на измервателните сигнали са установени от GOST 16465-70 "Радиотехнически сигнали. Термини и определения". Измервателните сигнали са изключително разнообразни. Тяхната класификация по различни характеристики е показана на фиг. 10.1.
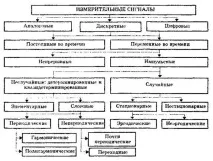
Ориз. 10.1. Класификация на измервателните сигнали
Споредестеството на измерване на информативни и времеви параметриизмервателните сигнали се разделят на аналогови, дискретни и цифрови.
Аналогов сигнале сигнал, описан от непрекъсната или частично-непрекъсната функция Ya ( t ), като както самата тази функция, така и нейният аргумент t могат да приемат всякакви стойности на дадените интервали Y н ( Ymin ; Ymax ) и t н ( tmin ; tmax ) (фиг. 10.2,а).

Ориз. 10.2. Аналогов (а), дискретен (по време) (б)
и цифрови (в) измервателни сигнали
Дискретният сигнале сигнал, който варира дискретно във времето или нивото. В първия случай той може да получи n T в дискретни времена, където T = const е интервалът на вземане на проби (период), n = 0; 1; 2;. - цяло число, всякакви стойности Y d ( nT ) н ( Yniin ; Ymax ), нареченипроби,илиброи.Такива сигнали (фиг. 10.2,6) се описват от решетъчните функции. Във втория случай стойностите на сигнала Ya ( t) съществуват във всеки момент от време t н ( tmin ; tmax ), но те могат да приемат ограничен брой стойности hi = nq, които са кратни на кванта q .
Цифровите сигналиса квантувани по ниво и дискретни по време сигнали Yu ( nT ), които се описват от квантувани решетъчни функции (квантувани последователности), които в дискретни времена nT приемат само крайна поредица от дискретни стойности - нива на квантуване h 1 , h 2 , . hn (фиг. 10.2, c).
Тези сигнали са разгледани подробно в разд. 10.5.
Споредхарактера на промяна във времето, сигналите се разделят напостоянни,стойностите на които не се променят във времето, ипроменливи,стойностите на които се променят във времето. DC сигналите са най-простият тип измервателни сигнали.
Променливите сигнали могат да бъдат непрекъснати във времето и импулсни.Непрекъснате сигнал, чиито параметри се променят непрекъснато.Импулсенсигнал е сигнал с крайна енергия, значително различна от нула за ограничен интервал от време, съизмерим с времето на завършване на преходния процес в системата, върху който този сигнал е предназначен да въздейства. Характеристиките и параметрите на импулсните сигнали са разгледани в раздел. 10.4.
Споредстепента на наличие на априорна информацияпроменливите измервателни сигнали се разделят на детерминистични, квазидетерминирани и случайни.Детерминиран сигнале сигнал, чийто закон на промяна е известен и моделът не съдържа неизвестни параметри. Моментните стойности на детерминистичен сигнал са известни по всяко време. Детерминирани (с известна степен на точност) са сигналите на изхода на мерките. Например, изходът на нискочестотен генератор на синусоидахарактеризиращ се със стойности на амплитудата и честотата, които са зададени на неговите контроли. Грешките в настройката на тези параметри се определят от метрологичните характеристики на генератора.
К вазодетерминираните сигналиса сигнали с частично известен характер на промяна във времето, т.е. с един или повече неизвестни параметри. Те са най-интересни от гледна точка на метрологията. По-голямата част от измервателните сигнали са квазидетерминирани.
Детерминистичните и квазидетерминистичните сигнали се разделят наелементарни,описани с най-прости математически формули исложни.Елементарните сигнали включват постоянни и хармонични сигнали, както и сигнали, описани чрез единица и делта функции. Те се считат за секта. 10.3. Сложните сигнали включват импулсни и модулирани сигнали, описани в раздел. 10.4.
Сигналите могат да бъдатпериодични и непериодични.Непериодичните сигнали се делят на почти периодични и преходни.Почти периодичене сигнал, чиито стойности се повтарят приблизително, когато към аргумента време се добави правилно избрано число, почти период. Периодичният сигнал е специален случай на такива сигнали. Почти периодичните функции се получават чрез събиране на периодични функции с несъизмерими периоди, например Y ( t ) = sin ( w t ) + sin ( Ö 2 ̅ w t ).Преходнитесигнали описват преходни процеси във физически системи.
Периодичене сигнал, чиито моментни стойности се повтарят на постоянен интервал от време.Период Tна сигнала е параметър, равен на най-малкия такъв интервал от време,Честотаfна периодичен сигнал е реципрочната стойност на периода.
Периодичният сигнал се характеризира сспектър.Има три вида спектър:
•комплексе сложна функция на дискретен аргумент, който е кратно на цяло число честотни стойности o> периодичен сигнал Y ( t ), който е стойностите на коефициентите на сложната серия на Фурие:
(10.1)
където k е всяко цяло число;
•амплитудае функция на дискретен аргумент, който е модулът на комплексния спектър на периодичен сигнал:
(10.2)
където Re ( z ), Im ( z ) са реалната и имагинерната част на комплексното число z ;
•phaseе функция на дискретен аргумент, който е аргумент на комплексния спектър на периодичен сигнал:
(10.3)
Периодичният сигнал съдържа определен брой хармоници.Хармоници— хармоничен сигнал с амплитуда и начална фаза, равни на съответните стойности на амплитудния и фазовия спектър на периодичен сигнал при определена стойност на аргумента. Наличието на висши хармоници в спектъра на периодичен сигнал се описва количественочрез хармоничния коефициент,характеризиращ разликата във формата на даден периодичен сигнал от хармоничен (синусоидален). То е равно на съотношението на RMS стойността на сумарния сигнал на всички негови хармоници, с изключение на първия, към RMS стойността на първия хармоник:
(10.4)
където Yi , Y 1 са i-тия и първия хармоник на сигнала Y ( t ).
Периодичните сигнали сахармонични,т.е. съдържащи само един хармоник иполихармонични,спектърът на които се състои от много хармонични компоненти. Хармоничните сигнали включват сигнали, описани от функция синус или косинус. Всички останали сигнали са полихармонични.
Случайният сигнале променливавремето е физическа величина, чиято моментна стойност е случайна променлива. Характеристиките и параметрите на случайните сигнали или, както се казва, процесите, са разгледани в раздел. 4.3.
Обширна научна литература е посветена на измерването на сигнали. Пример е [89, 90].