Урок по алгебра на тема - Уравнения с параметър

Секции: Математика

Цели: да се изучи понятието "уравнения с параметър", да се формира способност за решаване на линейни и квадратни уравнения с параметър.

Мястото на урока в работната програма:

Извършете или преди контролна работа № 6 "Дробно-рационални уравнения", или след нея.

Урок за провеждане в клас с добра математическа подготовка. За учениците, които се обучават на "3", можете да подготвите индивидуални задачи с цел коригиране на грешки от контролната работа.

Напредък на урока

Аз. Проверка на домашното (Приложение 1, слайдове 2-14).

1) Карти, които бяха раздадени на учениците в предишния урок. (Приложение 2 ).

2) От учебник номер 703

II. Въведение в темата на урока.

Реши кръстословицата. Задачите се четат от учителя. Проверка (Приложение 1,слайдове 15-16 )

1. Графиката на квадратична функция е ...

2. Равенство, съдържащо променлива, чиято стойност трябва да се намери, е ...

3. Квадратно уравнение, в което коефициентът при x 2 е равен на 1, се нарича ...

4. Уравнения, в които лявата и дясната страна са рационални изрази, се наричат ...

5. Писането на правило с помощта на букви е ...

6. Графиката на функцията y \u003d k / x, където x ≠ 0, е ...

7. Теорема, изразяваща връзката между коефициентите на квадратно уравнение и неговите корени, се нарича теорема ...

8. Уравнение под формата ax 2 + inx + c \u003d 0, където x е променлива, a, b и c са някои числа и a≠0 се нарича ....

Записахме темата на урока. (Приложение 1, слайд 17)

Колко корена може да има едно линейно уравнение в зависимост от коефициентите? Какво ще кажете за квадрат?

III. Обяснениенов материал.

1. Изучаването на понятието "уравнение с параметър".

По време на актуализирането на знанията учениците запомниха, че едно линейно уравнение в зависимост от коефициентите може да има едно решение, безкрайно много решения или да няма решения. По същия начин, квадратно уравнение, в зависимост от дискриминанта и следователно от коефициентите, може да има един корен, два корена или да няма корени.

(Приложение 1, слайд 18)

Определение. Уравнение под формата f (a, b, c ..., x) \u003d 0, променливите a, b, c ..., които са постоянни при решаването на уравнението, се наричат параметри, а самото уравнение - уравнение с параметри.

Ако уравнението е написано като равенство на два израза, чийто запис включва две букви, например брадва = 5, тогава трябва ясно да определите какъв вид уравнение е това. Има три значения:

1) x, a са еквивалентни променливи. Казват, че е дадено уравнение с две променливи и се изисква да се намерят всички двойки (x, a), които удовлетворяват това уравнение.

2) x е променлива, a е фиксирано число. Казваме, че ни е дадено уравнение с една променлива x и трябва да намерим стойността на x, която удовлетворява уравнението за фиксирана стойност на a.

3) x е променлива, a е всяко число от някакъв набор A. Казват, че е дадено уравнение с променлива x и параметър a (A е набор от промени на параметри), изисква се да се реши уравнението за x за всяка стойност на a.

Диапазонът на параметъра или е зададен предварително, или обикновено се има предвид наборът от всички реални числа.

Тогава проблемът за решаване на уравнение с параметър може да бъде преформулиран: решетесемейството от уравнения, получени от уравнението за всякакви реални стойности на параметъра.

2. Да вземем решения на уравнението с параметър.

ясно,че е невъзможно да се запише всяко уравнение от безкрайно семейство уравнения. Всяко семейно уравнение обаче трябва да бъде решено. Това може да стане, ако според някакъв разумен критерий наборът от всички стойности на параметъра се раздели на подмножества и след това даденото уравнение се решава на всяко от тези подмножества.

За да разделите набора от стойности на параметри на подгрупи, е удобно да използвате тези стойности на параметри, при които или при преминаване през които настъпваткачествени промени на уравнението. Такива стойности на параметри се наричат контрол.

3. Алгоритъм за решаване на уравнение с параметър:

Стъпка 1. Намерете областта на промяна на параметъра.

Стъпка 2. Намираме уравнението ODZ.

Стъпка 3. Ние определяме контролните стойности на параметъра и разделяме областта на промяна на параметъра на подмножества.

4-та стъпка Решаваме уравнението за всяко подмножество от диапазона на параметрите.

Стъпка 5 Запишете отговора.

4. Решаване на линейни и квадратни уравнения с параметър.

За примери от стр. 141–143 от учебника, помислете как се намират контролните стойности на параметъра, как с тяхна помощ наборът от стойности на параметрите се разделя на подмножества и след това как даденото линейно или квадратно уравнение се решава на всяко от подмножествата.

IV. Формиране на умения и способности.

Всички упражнения, свързани с този параграф, могат да бъдат разделени на 3 групи:

1) решаване на уравнение с параметър, даден в стандартна форма;

2) трансформира уравнението с параметъра и го решава;

3) намерете стойностите на параметрите, при които ще бъде изпълнено дадено условие.

1. No 641 (а) (Учителят анализира заедно с учениците).

Ако p \u003d 0, тогава уравнението ще приеме формата -1 \u003d 0.

дадениуравнението няма корени.

Отговор: при p = 0 няма корени; при p ≠ 0; y = (p + 1)/p.

2. № 642 (Ученик, който сам се включи на борда).

Ако a - 2 \u003d 0, тоест a \u003d 2, тогава

Ако a - 2 ≠ 0, т.е. a ≠ 2, тогава x \u003d (a-2) (a 2 -9) / (a-2),

Отговор: при a = 2 x - всяко; с a ≠ 2 x \u003d a 2 - 9.

№ 644 (b) (Анализът се извършва и след това го записваме).

Ако a ≠ 0, тогава D > 0 и

3. № 646 (Извършваме анализ и даваме време да решим сами, след което проверяваме).

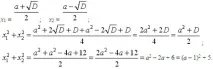
x1 2 + x2 2 приема най-малката стойност при a = 1 и е равно на 5.

Отговор: 5 с a = 1.

V. Физическо възпитание (Приложение 3, Приложение 4, Приложение 1, слайд 20)

VI. Учебна самостоятелна работа.

№ 645 (б) - I вариант, № 645 (d) - II вариант.

Двама ученика на сгъваеми дъски. Оценки само за учениците, които са писали на "5".

VII. Обобщение на урока

Какви уравнения научихме днес?
Кое уравнение се нарича уравнение с параметър? (Слайд с дефиниция). Дайте вашите примери.
Уравнения с параметри се намират в изпитите за 9 и 11 клас. (Можете да предложите домашни задачи от GIA).

VIII. Домашна работа. (Приложение 1, слайд 22)

Прочетете точка 27 и анализирайте примери 1 и 2, № 645 (а, в), № 704.

Информационни ресурси:

Алгебра, 8 клас: учебник. за общо образование институции / [Yu.N. Макаричев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов]; изд. S.A. Теляковски. – 19-то изд. – М.: Просвещение, 2010.
Алгебра 8 клас. Задачи за обучение и развитие на учениците. / Lebedintskva E.A., Belenkova E.Yu. – М.: Интелект-Център, 2007.
Алгебра. 8 клас: планове на уроци по учебника на Ю.Н. Макаричева, Н.Г. Миндюк,К.И. Нешков, С.Б. Суворова (CD) - издателство "Учител". 2011 г.
Интернет ресурси.