Урок по математика - Алгебрични и аритметични начини за решаване на задачи
Цели:
- въведе различни начини за решаване на проблеми;
- дават идеи за алгебричния метод на решаване,
- да научи децата да избират различни начини за решаване, да съставят обратни проблеми.
Задачи:
- развиват логическо мислене
- развитие на мисловни операции, като анализ, синтез.
1. Загрейте
(Учениците стоят на местата си, учителят задава въпрос, ако ученикът е отговорил правилно, след това сяда).
- Какво е уравнение?
- Какво означава да намериш корена на уравнението
- Как да намерим неизвестния множител? Разделител? Minuend?
- Продължете определенията: Скоростта е. За да намерите разстоянието, трябва да... За да намерите времето, трябва да...
2. Проверка на домашните
(Вкъщи децата потърсиха определения в справочниците: алгебра,аритметика, геометрия).
Какво изучава алгебрата? аритметика? геометрия?
- Алгебрата–е наука, която изучава въпроси на уравнения и неравенства.
- Геометрията е една от най-старите части на математиката, изучаваща пространствените отношения и формите на телата.
- Аритметиката е наука за числата и операциите с тях.
(Ще ни трябват тези термини по-късно в урока.)
3. Изслушайте задачата
Всяка от четирите клетки съдържа 1 животно. На всяка клетка има надписи, но нито един не отговаря на действителността. Посочете кой е във всяка клетка. Поставете животните в техните клетки (всяко дете има наборно платно и карти с животни).
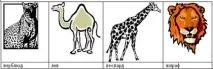
- Покажи какво имаш. Как разсъждавахте?(Извършете проверка на борда).
- Как решитази задача?(Разсъждение, логично мислене).
- Каква е задачата?(Булев).
Но най-вече в часовете по математика решаваме задачи, в които е необходимо да се извършват математически трансформации.
4. Прочетете задачите
- От две камили са остригани 12 кг вълна. От втория режат 3 пъти повече отколкото от първия. Колко килограма вълна е остригана от всяка камила?
- Леопардът тежи 340 кг, жирафът е 3 пъти по-тежък от леопард, а лъвът е със 790 кг по-лек от жирафа. Колко килограма е по-тежък леопард от лъв?
- Два жирафа тичаха един към друг. Единият тичаше със скорост 12 m/s, другият бягаше със скорост 15 m/s. След колко секунди ще се срещнат, ако разстоянието между тях е 135 метра?
Сравнете задачи. Какво общо? Какви са техните различия?
- Прочетете задачата, която трябва да решите, като съставите уравнение.
- Прочетете проблема, който трябва да бъде решен чрез действия?
- Какъв проблем може да се реши по два начина?
- Посочете темата на нашия урок.
Различни начини за решаване на проблеми
5. Решете всеки проблем, като направите кратка бележка (под формата на таблица, чертеж)
Двама души работят на дъската.
Проверете
- Как решихте първия проблем? (Уравнение).
- Как се нарича разделът на математиката, който се занимава с уравнения?(Алгебра).
- Как ще се нарича това решение?(алгебричен).
- Как бяха решени втората и третата задача?(Чрез действие).
- Кой клон на математиката изучава това?(Аритметика).
- Как ще се нарича това решение?(Аритметика).
(Виси се на дъската):
6. Съставете обратни задачи с данни и ги решавайте по алгебричен и аритметичен начин
7.Продуктивни задачи за възпроизвеждане на нови знания
Задавайте въпроси на класа по темата.
- Кой начин за решаване на задачи се нарича алгебричен?
- Каква аритметика?
- Какво е името на метода за решаване на проблеми с помощта на уравнения?
8. Домашна работа
Напишете задача с животни, която може да бъде решена алгебрично.