Урок по темата "Експоненциална функция"
Автор: Морина Светлана Алексеевна.
Учител по математика MBOU средно училище № 5 на курортния град Железноводск
Урок по темата "Експоненциална функция"
Тип урок:урок за изучаване на нов материал.
Целта на урока:за осигуряване на условия за усвояване от всеки ученик на знания за експоненциалната функция, нейните свойства.
Образователни задачи:въвеждат понятието показателна функция, разглеждат нейните свойства; се научат да прилагат изучените свойства на показателната функция при решаване на конкретни задачи и упражнения.
развиват способността за сравняване, обобщаване, правилно формулиране на задачи и изразяване на мисли;
развиват логическо мислене, внимание и способност за работа в проблемна ситуация;
да формира познавателния интерес на учениците;
култивирайте постоянство в постигането на целта.
2.Изучаване на нова тема. 20 минути.
Фронтална работа (слайд 2)
- Като епиграф на нашия урок искам да предложа думите на Г. Лесинг "Спорете, грешете, грешете, но, за Бога, мислете и, макар и криво, да сами." Днес трябва много да разсъждавате, да правите изводи.
— В живота често се сблъскваме със зависимости между количествата. Оценката за теста зависи от броя и коректността на изпълнените задачи, покупната цена, количеството закупени стоки и цени. Някои зависимости са случайни, докато други са постоянни.
Нека разгледаме следните закони. (слайдове 3)
P
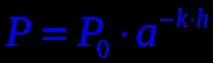
Налягането на въздуха намалява с надморска височина според закона:P— налягане на надморска височинаh,P0е налягането на морското равнище,ае някаква константа.
Какво е общото между тези процеси? (децата отговарят, като отбелязват сходството на типа формула, която определя закона)
-Нека поставим c=1, k=1 в тези формули, каква функция ще получим? (y \u003d a x) (слайд 4)
- Такава функция се нарича експоненциална.(Слайд 5)
- Днес в урока трябва да дефинираме експоненциалната функция, да разгледаме някои свойства и да научим как да прилагаме тези свойства при изпълнение на задачи от определен тип. (слайд 6)
— И така, опитайте се да формулирате дефиницията на експоненциална функция.
(учениците отговарят, учителят, ако е необходимо, коригира определението).
(Определение се появява на слайд 7, учениците го записват в тетрадка)
- В програмата Excel да се построят графиките на функциите y=2 x (вариант 1), y=(1/2) x на интервала [-2; 3] със стъпка 0,5. Според предложената схема (слайд 9), проучете функцията. (използват се таблици: опция график 1 и опция график 2)
1. Обхватът на функцията.
2. Диапазон от стойности на функцията.
3. Пресечни точки с координатните оси.
4. Интервали на нарастване и намаляване.
(Учителят говори накратко за Безопасност при работа с компютър. Учениците, работещи по двойки на компютри: съставят таблица, въвеждат x стойности, начертават графика на функция и разглеждат функцията по план. Таблицата „Вариант на графика 1” е представена така, както изглежда в началото на практическата работа, а „Вариант на графика 2” - както в края. Свойствата на функцията са написани на листове.)
Проверка на резултатите от практическата работа (Слайдове 10-11)
На екрана се появяват графики на функции, учениците назовават свойствата, които са показани. Учениците си водят записки в тетрадките.
4. Динамиченпауза. 1 минута
(гимнастика за очите)
5. Затвърдяване на изученото.13 минути.
Устно (учениците избират верния отговор, обосновавайки избора) (слайдове 12-16)
1. Коя от следните формули дефинира експоненциална функция?
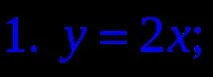
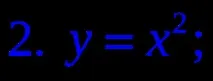
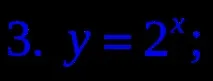
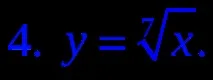
2. Дадена е графика на функция. Посочете тази функция
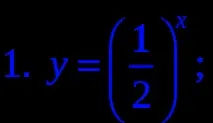
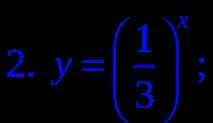
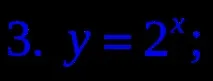
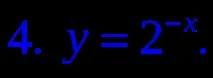
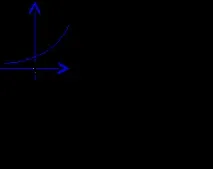
3. Посочете нарастваща функция.
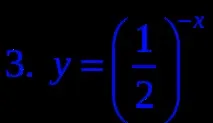
4. Посочете намаляваща функция.
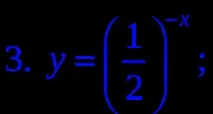
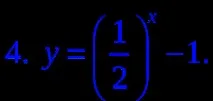
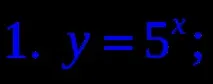
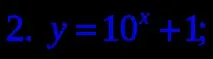
6.Намерете диапазона на функцията y=4 x -1. (слайдове 17-18)
Учениците намират диапазона от стойности, използвайки трансформации на графиката на функцията. Всички конструкции се правят от учениците в техните тетрадки.
2 решение.
2 x > 0 за всички x,
Формулиране на правилото (слайдове 19-20)
- Функцията е дадена: y \u003d a x ± b. Изведете правило, което позволява
без да се изпълнява конструкцията на графиката на тази функция,
намерете диапазона на функцията.
Ако y \u003d a x + b, тогава E (y) \u003d (b; +∞)
Ако y \u003d a x -b, тогава E (y) \u003d (-b; +∞).
Изпълнете устно задачата от слайд 21. Запишете отговорите в тетрадка. След това направете самотест.
6. Обобщаване.3 минути.
Отражение на учебен материал.
- С каква функция се запознахте в урока?
- Дефиниране на експоненциална функция.
- Припомнете си свойствата на функцията.
Отразяване на дейностите на учениците.
Какъв тип работа ви хареса в клас? Защо?
— Какви трудности възникнаха?
7. Домашна работа. (слайд 22)1 минута.