Урок - Повдигнете на квадрат сумата от няколко члена
Кратко описание на документа:
Стандартните формули за съкратено умножение са предназначени за работа с биноми и сравнително прости (според основната конструкция) полиноми. Понякога обаче, когато решавате по-сериозни проблеми, трябва да се справите с по-сложни операции.
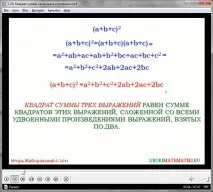
(a + b + c) 2 = (a + b + c)(a + b + c) =
\u003d a 2 + ab + ac + ab + b 2 + bc + ac + bc + c 2 \u003d
\u003d a 2 + b 2 + c 2 + 2ab + 2ac + 2bc
За практика ще изучим новата формула в упражнението. Изчислете стойността на квадрата:
Използвайки горното равенство, получаваме нов израз и отваряме скобите:
(2a + x + 3c) 2 = (2a) 2 + x 2 + (3c) 2 + 2(2ax) + 2(2a 3 s) + 2(x 3 s) =
\u003d 4a 2 + x 2 + 9c 2 + 4ax + 12ac + 6cx
Както можете да видите, прилагането на формулата за повдигане на квадрат на сумата от три израза е доста прост процес, който изисква само внимание, особено когато се умножават коефициенти.
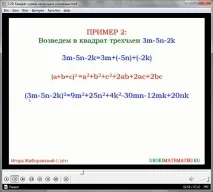
Тъй като сумата в скоби на формулата има алгебричен смисъл, това равенство може успешно да се приложи и към разликата на изразите - всъщност за всеки тричлен. За новото упражнение нека обърнем знаците в нашия първи пример:
За да решим този израз, използвайки формулата за квадрат на сумата, използваме разделянето на знаците на коефициентите в скоби, тоест записваме тринома под формата на алгебрично сумиране:
(2a - x - 3s) 2 \u003d (2a + (- x) + (- 3s)) 2
(2a + (- x) + (- 3c)) 2 \u003d (2a + (- x) + (- 3c)) (2a + (- x) + (- 3c)) \u003d
\u003d (2a) 2 + (-x) 2 + (-3c) 2 + 2 (-2ax) + 2 (-2a3c) + 2 (3cx) \u003d
\u003d 4a 2 + x + 9c 2 - 4ax - 12ac + 6cx
Ако се вгледате внимателно в отговора, можете да направите следното заключение: разликата в първоначалния израз доведе до факта, че две от триудвоените произведения на двойки изрази са получили знак минус. Всички други данни останаха същите. Струва си да се отбележи, че квадратът на всичко анулира минуса, така че първата част от сумата в отговора няма да зависи от знаците в първоначалния израз и винаги остава положителна. Нека усложним задачата и се опитаме да изчислим квадрата на сумата от четири израза. В този случай ще използваме стандартния FSO, за да улесним изчисленията:
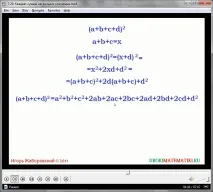
(a + x + y + c) 2 = ((a + x + y) + c) 2 =
\u003d (a + x + y) 2 + 2 (a + x + y) c + c 2
\u003d a 2 + x 2 + y 2 + 2ax + 2ay + 2xy + 2ac + 2xc + 2us + c 2 \u003d
\u003d a 2 + x 2 + y 2 + c 2 + 2ax + 2ay + 2ac + 2xy + 2xc + 2us
Крайният израз е формула за определяне на квадрата на сумата от четири израза. Или в устна форма: квадратът на сбора от четири естествени израза е равен на сбора от квадратите на тези изрази, добавен към двойните произведения на всички изрази, взети по двойки.
По този начин, повдигането на квадрат на всеки полином е доста стандартизирано и дава подобни резултати, така че може да се изведе обща формулировка, която работи за всеки краен брой изрази: Квадратът на сумата от няколко израза е сборът от квадратите на дадените изрази, добавен към удвоените продукти на всички изрази, взети като двойка. Разгледайте следния проблем. Нека повдигнем на квадрат израза:
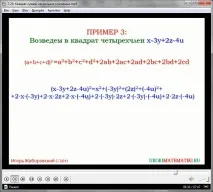
Използвайки получените формули или общата формула (работеща за всяка алгебрична сума), ние трансформираме и решаваме, отваряйки скобите и опростявайки:
(3 + x - 5y + 3s) 2 \u003d (3 + x + (- 5y) + 3s) 2 \u003d
\u003d (3 + x + (- 5y) + 3s) (3 + x + (- 5y) + 3s) \u003d
\u003d (3) 2 + x 2 + (-5y) 2 + (3s) 2 + 2(3x) + 2(-15y) + 2(9s) + 2(-5uh) + 2(3sx) - 30us
\u003d 9 + x 2 + 25y 2 + 9s 2 + 6x - 30y + 18s - 10uh + 6sh -30 us
Разбирането на общите принципи за извеждане на определени формули помага много при решаването на нетривиални упражнения, които имат подобна задача, но на по-високо ниво.