Вдлъбнатост и изпъкналост на функция, тангенс

Нека разгледаме други характеристики на функциите -вдлъбнатост и изпъкналост. Отново, това е интуитивна концепция, защото всеки знае кога една повърхност е вдлъбната и кога е изпъкнала. Ако видим на масата предмет, който може да съдържа течност, казваме, че е вдлъбнат (като купа, например). Същият обект, ако се обърне и отново

постави на масата, ще ни покаже изпъкнала повърхност. Тоест вдлъбнатите повърхности са по-далеч от нас, а изпъкналите са по-близо. Но зависи от гледната точка. Един и същи обект може да бъде вдлъбнат или изпъкнал, в зависимост от това от коя страна го гледате.

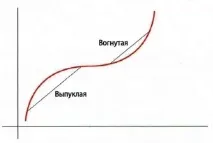
При функциите се прилага следният подход: „изправяме се“ по хоризонталната ос и гледаме нагоре. И това е всичко. Въпреки това все още се нуждаем от по-строга дефиниция. За да го получим, ще направим следното. Вземете произволни две точки от кривата и ги свържете с хорда. Ако функцията е разположена на върха на хордата, тогава тя е изпъкнала в интервала, определен от точките; и ако е отдолу, значи е вдлъбнат.

Вдлъбнатостта и изпъкналостта са характеристики, които са свързани сконцепцията за кривина, тъй като те уникално дефинират посоката на кривина на графиката на кривата.

Точката, в която функцията се променя от вдлъбната към изпъкнала или обратно, се наричаинфлексна точка.

Едно от най-големите открития, направени в изследването на функциите, беше аналитичнатадефиниция на допирателна, т.е. дефиницията на уравнението на допирателна линия в точка от дадена крива. Като цяло можем да кажем, че допирателната е линия, която докосва кривата в една точка, без да я пресича.

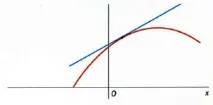
Нека видим какво се случва с тангентата, когато се доближим до максимума.

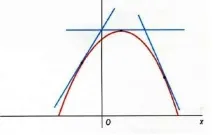
Виждаме, че допирателната образува ъгъл по-малък от 90° с оста OX в тези интервали, къдетофункцията нараства и ъгълът е по-голям от 90° в интервалите, където функцията намалява. Променяйки наклона си, тангентата със сигурност ще премине прездопирателната точка, където, намирайки се в хоризонтално положение, ще сключва ъгъл 0° с абсцисната ос. Това се случва винаги, когато изпълним максимума. Същото се случва и в минималните точки, тъй като допирателната, минаваща през тях, също е хоризонтална. Но хоризонталността на допирателната в дадена точка не е гаранция, не е достатъчно условие за това, че в тази точка функцията преминава максимум или минимум. Може да се случи, че говорим за точка на инфлексия - за точката, която разделя вдлъбнатата зона от изпъкналата. Въпреки това, в ситуация, в която ъгълът между допирателната и оста x е нула, винаги е възможно да се определи аналитично дали това е граница (максимум или минимум) или инфлексна точка.