Връзки и указатели
Цел: изследване на фундаменталната абстрактна структура - свързани списъци.
В днешния урок ще разгледаме фундаменталната абстрактна структура на свързан списък.
Свързаният списък е колекция от последователно организирани данни. Свързаните списъци се дефинират като примитиви в някои езици за програмиране (напр. Lisp, Delphi), но не и в Pascal. Pascal обаче предоставя някои основни примитивни операции, за да улесни използването на свързани списъци.
Основното предимство на свързаните списъци пред масивите е, че те могат да растат или да се свиват по време на изпълнение на програмата. По-специално, не е необходимо да знаем максималния му размер предварително.
Второто предимство е, че осигуряват гъвкавост за пренареждане на елементите си. Тази гъвкавост идва за сметка на скоростта на достъп до произволен елемент от списъка. Това ще стане по-ясно по-късно, след като разгледаме някои от основните свойства на свързаните списъци и основните операции, дефинирани върху тях.
Списъкът може да бъде представен като връзки във верига.
В масив се предоставя последователна организация директно (според индекса).
Свързаният списък използва специален начин за организиране на данни, според който неговият елемент се съдържа в „възел“, съдържащ данни, както и „връзка“ към следващия „възел“.
Възел и връзка могат да бъдат описани по следния начин:
Тип Връзка = ^Възел; Възел = запис Данни: цяло число; Следва: Връзка; Край;
За да опишем списъка, ще използваме два допълнителни помощни възела head и z. Главният възел ще сочи към първия елемент от списъка, а z ще сочи към последния елемент от списъка. Глава понякогасе нарича "глава" на списъка, а z се нарича "опашка".
Тогава списъкът може да бъде представен в следната форма.
Това представяне на данни ви позволява да извършвате някои операции с много по-ефективни методи, отколкото с масиви. Например, ако искаме да преместим елемент 1 от края към началото, тогава, за да извършим такава операция в масив, ще трябва да преместим всички негови елементи, за да освободим място. В свързания списък променяме само връзките. И двете версии на фигурата са еквивалентни; те просто са нарисувани по различен начин. Ние просто нулираме връзката на възела, съдържащ 1, към възела, съдържащ 2, и връзката на празния главен възел към възела, съдържащ 1. Дори ако списъкът беше много голям, пак ще ни трябват само три пермутации на връзката за такъв обмен.
 |
По-важното е, че вече можем да говорим за "вмъкване" на елемент в свързан списък (което увеличава дължината му с един елемент) - операция, която е толкова неестествена и неудобна за масиви. Фигурата показва как да вмъкнете нов възел в списъка. Първо трябва да добавите този възел, след това да създадете връзка към възел q и след това да промените връзката на възел p към новия възел. Това изисква само две препратки да бъдат променени, независимо от дължината на списъка.
 |
По подобен начин можем да говорим за "премахване" на елемент от списъка (което намалява размера му с един елемент). Просто трябва да промените връзката към възела, който следва възела q и след това възелът, съдържащ q, трябва да бъде унищожен.
 |
Pascal ни предоставя някои примитивни операции, които ни позволяват да създаваме директно свързани списъци. Следният кодов фрагмент е пример за изпълнение на основните функции,които току-що обсъдихме.
Тип Връзка = ^Възел; Възел = запис Данни: цяло число; Следва: Връзка; Край;
Var Head, z: връзка;
процедура list_initialize; започнете ново(глава); ново(z); head^.next := z; z^.next := нула; край;
процедура insert_after( v : цяло число; t : връзка ); вар. x : връзка; начало ново(x); x^.data := v; x^.next := t^.next; t^.next := x; край;
процедура delete_next( t : връзка ); var del: връзка; започнете дел := t^.next; t^.next := t^.next^.next; изхвърляне(дел); край;
Нека ги разгледаме по-подробно.
Link = ^Node; - тук се създава нов тип Link, който е въведен указател към типа Node. Типът възел е показан по-долу.
Нека разгледаме по-отблизо това определение.
Компютърната памет може да бъде представена по следния начин. Той е разделен на блокове, всеки такъв блок се нарича сегмент. В Dos всеки номер на сегмент може да съдържа максимум 16 бита (числото $FFFF, когато всички битове са равни
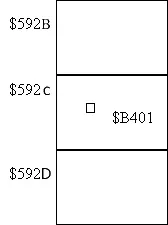 |
1) (символът $ е знак на шестнадесетичната система), т.е. всеки сегмент може да има номер [0; $FFFF]. Да приемем, че разглеждаме област на паметта със сегменти $592B, $592C, $592D. За да намерите конкретна клетка от паметта във всеки сегмент, има така нареченото отместване, което също може да бъде номерирано [0; $FFFF]. Например, нека отместването вътре в сегмента $592C е $B401, тогава указателят към това място в паметта ще бъде $592CB401.
procedure list_initialize;
head^.next := z; - тук въвеждаме $592CB401 в клетката, започвайки от 3 байта (тъй като първите два са заети от ключ) в областта, наречена Next, числото $592D000A.
 |