Въведение в анализа на сложността на алгоритмите (част 1)
От преводача: този текст е даден с незначителни съкращения поради прекомерно "сдъвкания" материал на места. Авторът напълно основателно предупреждава, че някои теми ще изглеждат твърде прости или добре известни. Въпреки това, този текст ми помогна лично да рационализирам съществуващите знания за анализа на сложността на алгоритмите. Надявам се да е полезно и на някой друг. Поради дължината на оригиналната статия я разделих на четири части. Аз (както винаги) ще бъда изключително благодарен за всякакви коментари в ЛС за подобряване на качеството на превода.
Много съвременни програмисти, които пишат готини и широко разпространени програми, имат много неясна представа за теоретичната компютърна наука. Това не им пречи да бъдат отлични креативни специалисти и ние сме благодарни за това, което създават.
Познаването на теорията обаче също има своите предимства и може да бъде много полезно. В тази статия, предназначена за програмисти, които са добри практици, но имат малко разбиране на теорията, ще представя един от най-прагматичните инструменти за програмиране: нотация Big O и анализ на сложността на алгоритъма. Като човек, който е работил както в академичните среди, така и в разработката на търговски софтуер, намирам тези инструменти за наистина полезни на практика. Надявам се, че след като прочетете тази статия, ще можете да ги приложите към собствения си код, за да го направите още по-добър. Освен това тази публикация ще донесе със себе си разбиране на такива често срещани термини, използвани от теоретиците на компютърните науки като „голямо О“, „асимптотично поведение“, „анализ на най-лошия случай“ и т.н. Този текст е насочен и към гимназисти от Гърция или друга странаучастие в международна олимпиада по информатика, състезания по алгоритми за ученици и др. Като такъв, той не изисква предварително познаване на сложни математически концепции и просто ще ви даде основа за по-нататъшно изследване на алгоритми със солидно разбиране на теорията зад тях. Като човек, който се е състезавал много в миналото, горещо ви препоръчвам да прочетете и разберете целия уводен материал. Тези знания ще бъдат незаменими, докато продължавате да изучавате алгоритми и различни съвременни технологии.
Нотацията Big O и анализът на сложността на алгоритмите са неща, които както практичните програмисти, така и начинаещите студенти често смятат за трудни за разбиране, страх или като цяло избягват като безполезни. Но те не са толкова сложни и сложни, колкото може да изглежда на пръв поглед. Сложността на един алгоритъм е просто начин за формално измерване на това колко бързо работи дадена програма или алгоритъм, което е много прагматична цел. Нека започнем с малко мотивация по тази тема.
Вече знаем, че има инструменти, които измерват колко бързо се изпълнява кодът. Това са програми, наречениprofilers(profilers), които определят времето за изпълнение в милисекунди, като ни помагат да идентифицираме тесните места и да ги оптимизираме. Но въпреки че е полезен инструмент, той няма нищо общо със сложността на алгоритмите. Сложността на алгоритъма е нещо, което се основава на сравняване на два алгоритъма на идеално ниво, като се игнорират детайли от ниско ниво, като внедряването на езика за програмиране, хардуера, на който програмата работи, или набора от инструкции на даден процесор. Искаме да сравним алгоритмите по отношение на това, което всъщност представляват: идеи за това как работи изчислението. Броенето на милисекунди не помага много тук. Може и добреоказва се, че лош алгоритъм, написан на език от ниско ниво (като асемблер), ще бъде много по-бърз от добър алгоритъм, написан на език за програмиране от високо ниво (като Python или Ruby). Така че е време да решим кой всъщност е „най-добрият алгоритъм“.
Алгоритъмът е програма, която е чисто изчислителна, без други неща, които компютърът често прави, като например мрежови задачи или потребителски вход/изход. Анализът на сложността ни позволява да разберем колко бърза е тази програма, когато прави изчисленията. Примери за чистоизчислителниоперации са операции с плаваща запетая (събиране и умножение), търсене на дадена стойност от база данни в RAM, определяне на изкуствения интелект (AI) на играта, за да премести своя герой, така че да се движи само на кратко разстояние в света на играта, или изпълнение на модел на регулярен израз срещу низ. Ясно е, че изчисленията са повсеместни в компютърните програми.
Анализът на сложността също така ни позволява да обясним как ще се държи алгоритъмът при увеличаване на входните данни. Ако нашият алгоритъм работи за една секунда с 1000 входа, как ще се държи, ако удвоим тази стойност? Ще работи ли също толкова бързо, един път и половина по-бързо или четири пъти по-бавно? В практиката на програмирането подобни прогнози са изключително важни. Например, ако създадохме алгоритъм за уеб приложение с хиляда потребители и измерихме времето му за изпълнение, тогава с помощта на анализ на сложността получаваме доста добра представа какво се случва, когато броят на потребителите се увеличи до две хиляди. За състезания по конструиране на алгоритми, анализ на сложносттасъщо така ще ни даде представа колко дълго ще работи нашият код на най-големия от тестовете, за да проверим неговата коректност. Така че, ако определим общото поведение на нашата програма върху малко количество входни данни, можем да получим добра представа какво ще се случи с нея при големи потоци от данни. Нека започнем с прост пример: намиране на максималния елемент в масив.
Брой инструкции
В тази статия ще използвам различни езици за програмиране, за да реализирам примерите. Не се притеснявайте, ако не сте запознати с някой от тях - всеки, който знае как да програмира, трябва да може да прочете този код без много проблеми, защото е прост и няма да използвам никакви екзотични езикови дрънкулки за имплементация. Ако сте ученик на олимпиада, най-вероятно пишете на C ++, така че и вие не трябва да имате проблеми. В този случай препоръчвам също така да работите с упражненията, като използвате C++ за повече практика.
Максималният елемент на масив може да бъде намерен с помощта на най-простия код. Например такъв, написан на Javascript. Даден входен масив A с размер n:
Първо, нека изчислим колкофундаментални инструкцииса изчислени тук. Ще направим това само веднъж - като навлезем по-дълбоко в теорията, тази нужда ще изчезне. Но засега бъдете търпеливи с времето, което отделяме за това. В процеса на анализиране на този код има смисъл да се раздели на прости инструкции - задачи, които могат да бъдат изпълнени от процесора веднага или близо до него. Да предположим, че нашият процесор е в състояние да изпълни следните операции като единични инструкции:
- Присвояване на стойност на променлива
- Намерете стойността на конкретен елемент в масив
- Сравнете две стойности
- стойност на нарастване
- Основни аритметични операции (като събиране и умножение)
Необходими са две инструкции: да се търси A[0] и да се присвои стойност на M (приемаме, че n винаги е поне 1). Тези две инструкции ще се изискват от алгоритъма, независимо от стойността на n. Цикълът for също ще бъде инициализиран през цялото време, което ни дава още две команди: присвояване и сравнение.
Всичко това се случва преди първото изпълнение на за . След всяка нова итерация ще имаме още две инструкции: увеличение i и сравнение, за да проверим дали е време да спрем цикъла.
По този начин, ако пренебрегнем съдържанието на тялото на цикъла, тогава броят на инструкциите за този алгоритъм е 4 + 2n - четири в началото на цикъла for и две за всяка итерация, от които имаме n части. Сега можем да дефинираме математическа функция f(n), така че, знаейки n, да знаем и броя на инструкциите, изисквани от алгоритъма. За for цикъл с празно тяло, f(n) = 4 + 2n.
Анализ на най-лошия случай
В тялото на цикъла имаме операции за търсене и сравнение на масиви, които винаги се случват:
Но тялото на if може или не може да се изпълнява в зависимост от действителната стойност в масива. Ако се случи A[ i ] >= M , тогава ще изпълним две допълнителни команди: търсене в масив и присвояване:
Вече не можем да дефинираме f(n) толкова лесно, защото сега броят на инструкциите зависи не само от n, но и от конкретни входни стойности. Например, за A = [ 1, 2, 3, 4 ] програмата ще изисква повече инструкции, отколкото за A = [ 4,3, 2, 1]. Когато анализираме алгоритми, най-често вземаме предвид най-лошия сценарий. Какво ще бъде в нашия случай? Кога алгоритъмът ще се нуждае от най-много инструкции, за да изпълни? Отговор: когато масивът е сортиран във възходящ ред, като A = [ 1, 2, 3, 4 ] . Тогава M ще бъде преназначаван всеки път, което ще дава най-много команди. Теоретиците имат фантастично име за това -анализ на най-лошия случай, което не е нищо повече от просто разглеждане на най-лошия сценарий. Така в най-лошия случай се изпълняват четири инструкции в тялото на цикъла от нашия код и имаме f( n ) = 4 + 2n + 4n = 6n + 4 .
Асимптотично поведение
С горната функция имаме доста добра представа колко бърз е нашият алгоритъм. Въпреки това, както обещах, не е нужно постоянно да се занимаваме с толкова досадна задача като броенето на инструкции в програма. Освен това броят на инструкциите за конкретен процесор, необходими за прилагане на всяка разпоредба от използвания език за програмиране, зависи от компилатора на този език и набора инструкции, достъпен за процесора (AMD или Intel Pentium на персонален компютър, MIPS на Playstation 2 и т.н.). По-рано казахме, че ще игнорираме подобни условия. Така че сега ще прекараме нашата функция f през "филтър", за да я изчистим от незначителни детайли, на които теоретиците предпочитат да не обръщат внимание.
Нашата функция 6n + 4 има два елемента: 6n и 4 . При анализа на сложността единственото нещо, което има значение, е какво се случва с функцията за броене на инструкции, когато n се увеличи значително. Това съвпада с предишната идея за „най-лошия случай“: интересуваме се от поведението на алгоритъм в „лоши условия“, когатопринуден да направи нещо трудно. Обърнете внимание, че това е наистина полезно при сравняване на алгоритми. Ако един от тях победи другия с голям входен поток от данни, тогава е вероятно той да остане по-бърз при леки, малки потоци. Ето защоизхвърляме онези елементи от функцията, които нарастват бавно с нарастването на n, и оставяме само тези, които нарастват силно. Очевидно 4 ще остане 4 независимо от стойността на n, докато 6n, напротив, ще се увеличи. Така че първото нещо, което правим, е да изхвърлим 4 и да оставим само f(n) = 6n.
Има смисъл да мислим за 4 просто като за "инициализираща константа". Настройката на различните езици за програмиране може да отнеме различно време. Например Java първо трябва да инициализира своята виртуална машина. И тъй като се съгласихме да игнорираме разликите в езиците за програмиране, ние просто ще отхвърлим тази стойност.
Второто нещо, което трябва да игнорирате, е множителят пред n. Така нашата функция става f(n) = n. Както можете да видите, това опростява много. Още веднъж, постоянният фактор има смисъл да се отхвърли, ако мислим за разликите във времето за компилиране на различните езици за програмиране (PL). „Търсене в масив“ за един PL може да се компилира много по-различно от друг. Например в C изпълнението на A[ i ] не включва проверка дали i е в рамките на декларирания размер на масива, докато в Pascal го прави. Така че даденият паскал код е:
е еквивалентно на следното в C:
Така че има смисъл да се очаква, че различните езици за програмиране ще бъдат повлияни от различни фактори, които влияят на броя на инструкциите. В нашия пример, където използваме "безшумен" компилатор на Pascal, който игнориравъзможности за оптимизация, той изисква три инструкции в Pascal за всеки достъп до елемент от масив вместо една в C. Пренебрегването на този фактор върви в съответствие с игнорирането на разликите между конкретните езици за програмиране с фокус върху анализа на самата идея на алгоритъма като такъв.
Филтрите, описани по-горе - "премахване на всички фактори" и "запазване само на най-големия елемент" - заедно дават това, което наричамеасимптотично поведение. За f( n ) = 2n + 8 то ще бъде описано от функцията f( n ) = n . Говорейки на езика на математиката, ние се интересуваме от границата на функцията f, когато n клони към безкрайност. Ако не разбирате съвсем смисъла на тази официална фраза, тогава не се притеснявайте - вече знаете всичко, от което се нуждаете. (Освен: Строго погледнато, в математическа среда не бихме могли да отхвърлим константите в границата, но за целите на теоретичната компютърна наука го правим поради причините, описани по-горе). Нека да изпълним няколко задачи, за да разберем напълно тази концепция.
- f(n) = 5n + 12 ще даде f(n) = n. Причините са същите като описаните по-горе
- f(n) = 109 ще даде f(n) = 1. Изпускаме множителя 109 * 1, но 1 все още е необходимо, за да покаже, че функцията е различна от нула
- f( n ) = n 2 + 3n + 112 дава f( n ) = n 2 Тук n 2 расте по-бързо от 3n, което от своя страна расте по-бързо от 112
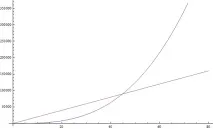
- f( n ) = n 3 + 1999n + 1337 дава f( n ) = n 3 Въпреки големия множител пред n, ние все още мислим, че можем да намерим още по-голямо n, така че f( n ) = n 3 все още е по-голямо от 1999n (вижте фигурата по-горе)
- f(n) = n + sqrt(n) ще дадеf( n ) = n Тъй като n расте по-бързо, когато неговият аргумент се увеличава от sqrt( n )