Въведение в метода Монте Карло
В тази статия няма да се задълбочаваме в математиката, а ще се опитаме да дадем обща представа за метода Монте Карло.
Същността на метода е следната: генерира се набор от случайни стойности за целевата случайна променлива и след това въз основа на нея се изчисляват необходимите стойности.
Методът Монте Карло има много различни приложения. Използва се в следните области: в индустрията за моделиране на променливостта на производствените процеси; по физика, химия и биология за моделиране на различни явления; в областта на симулационните игри с изкуствен интелект, като китайската игра Go; във финансите за оценка на деривативни финансови инструменти и опции. Всъщност методът Монте Карло се използва навсякъде.
Модерната версия на метода е създадена в рамките на проекта Манхатън, където е използвана за симулиране на разстоянията, които неутроните могат да изминат в различни материали. Идеята за моделиране, базирано на генерирането на набор от произволни стойности, съществува от известно време, но е особено развита по време на създаването на атомната бомба, след което се разпространява в много други области на знанието.
Голямото предимство на метода Монте Карло е, че ви позволява да вземете предвид елемента на случайност и сложността на реалния свят в модела. В допълнение, методът е стабилен по отношение на промяната на различни параметри, като например разпределението на случайна променлива. Основава се на закона за големите числа.
Един от типичните примери за използване на метода Монте Карло са задачи, при които е необходимо да се намери математическото очакване на някаква случайна променлива. За да направите това, трябва да генерирате набор от произволни стойности на дадено количество и да намерите средната стойност. Случайната променлива обикновено се характеризира с определено разпределениевероятности.
Изчисление на Пи
С помощта на метода Монте Карло можете да изчислите числото Пи. R кодът за този пример е тук.
Чрез вписване на кръг в квадрат (диаметърът на кръга е равен на страната на квадрата), можем да изразим съотношението на площта на кръга към площта на квадрата, както следва:
Ако можем да изчислим това съотношение, тогава можем да получим стойността на pi.
Нека запълним квадрата с точки с произволни координати. Нека изчислим отношението на броя точки в кръга към общия брой точки. Умножете резултата по 4, за да получите стойността на pi.

Колкото по-голям е броят точки, толкова по-близо е получената стойност до истинската стойност на Pi.
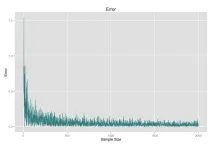
Този прост пример демонстрира метода Монте Карло в действие.
Моделиране на транспортния поток
Нека да разгледаме по-полезен пример. Можем да моделираме трафика с помощта намодела Nagel-Schreckenberg. В рамките на този модел маршрутът се състои от клетки, зададени са максимално допустимата скорост и определен брой превозни средства (ATS). На всяка стъпка статусът на всички телефонни централи се актуализира съгласно следните правила:
- Скоростта на дадения обмен v се увеличава с единица, ако е по-малка от максимално допустимата скорост.
- Нека намерим разстоянието d между дадения ATC и ATC отпред. Ако скоростта на това превозно средство е по-голяма или равна на разстоянието d, тя намалява до стойността d-1.
- Използвайки метода Монте Карло, нека добавим елемент на произволност. С вероятност p скоростта на даденото превозно средство намалява с единица.
- Този ATC се придвижва напред с v единици.
Този модел е доста прост, но много ефектен. Този модел не отчита аварии или лошошофиране. Целта му е да моделира спонтанни промени в характера на транспортните потоци. Има по-сложни модели, но много от тях са базирани на модела на Нагел-Шрекенберг.
Кодът за моделиране е тук, а за визуализация на езика Processing – тук.

Проблеми в рамките на метода Монте Карло
Основният проблем е генерирането на независими случайни променливи. Това не е толкова лесна задача, колкото може да изглежда на пръв поглед. В примерите с код ние просто извикахме вградените R или Python функции за генериране на произволни числа, но процесът може да бъде много по-сложен. Ако е необходимо, можете да се обърнете към научни източници по тази тема.
На тази връзка можете да намерите информация за това как се генерират случайни числа в R с равномерно разпределение.
Друг проблем е как да се осигури конвергенция на грешките. Имайте предвид, че в примера за изчисление на pi грешката е спряла да намалява. Повечето приложения на Монте Карло използват много големи проби за решаване на този проблем.