За концепцията за размит интеграл, Статия в списание "Млад учен"

Библиографско описание:
Въвеждането на концепцията за размит интеграл е свързано с желанието да се разработят аналози в размитата математика, използвани в статистиката и теорията на вероятностите за понятията средно и математическо очакване. Тъй като тези концепции се основават на свойството на адитивност на вероятностна мярка, а размитите мерки са по-широк клас от мерки, развитието на тези аналози доведе до изграждането на фундаментално нова математическа конструкция [2].
Размитият интеграл на функциятаh : X →[0, 1] върху множеството AX по отношение на размитата мярка g се дефинира като
h(x)g =(αg (A ∩Hα)), (1)
Размитият интеграл се нарича ощеразмито очакванеилиFEV (размита очаквана стойност).
Размитият интеграл на функциятаh : X →[0,1] върху размитото множествоA=A(x)>по отношение на размитата мярка g се дефинира като [3]
h(x)g =(μA (x) h(x))g(2)
Обърнете внимание наосновните свойства на размитите интеграли.
Некаa[0,1], (E, FX) иh: X→ [0,1].
1. .
2. .
3. .
4. .
5. .
6. .
Може да се покаже, че концепцията за размит интеграл е подобна на концепцията за интеграл на Лебег. За да направите това, помислете за разделянето на множеството X на непресичащи се подмножества (фиг. 1):, , i ≠ j, i=1,2,…,n.
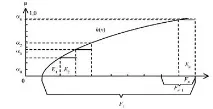
Ориз. 1. Построяване на стъпалната функция
Нека е стъпаловидно нарастваща функция (h:X →[0,1]), където
αi[0,1],ei x,feiе характеристичната функция на обичайния наборei, т.е.fei (x)= 1, акоxei, fei (x) = 0, x∉ ei.letлlebesge. Лебегов интеграл на функциятаhвърху множествотоAопределен като
, (3)
Нека въведем множестваFi =,i=1,2,…, n. Тогаваh(x)може да бъде представено като. В този случай размитият интеграл, по аналогия с интеграла на Лебег, може да се дефинира като:
. (4)
Сравнявайки (3) и (4), може да се намери сходство между тези интеграли: операциите събиране и умножение за интеграла (3) се заменят съответно с операциите max и min за (4) [1].
И двата интеграла - Лебегов и размит - могат да бъдат сравнени с помощта на вероятностна мярка. Ако(X, B, Р)е вероятностно пространство иh: X→ [0,1] еB-измерима функция, тогава имаме, че
. (5)
Сравнително лесно е да се изчисли размитият интеграл в случай на краен наборXи, съответно, крайно числоα, за което се изисква да се определиg(Hα).За да направите това, използвайте следното твърдение.
Ако функциятаh(x)приемаn+1стойността αi, тогава наборът отg(Hαi)стойности, различни от 0 и 1, съответно, се състои отnелементи. В последователност от2n+1елементи, съставени от елементи i>gt; и αi)>, подредени във възходящ ред, стойността на средния елементn+1е равна на стойността наFEV(h).
На фиг. Фигура 2 показва пример за графична интерпретация на намиране на стойността на размития интеграл за X = R [2]:
FEV(h)=,къдетоHα=h(x)≥α>.
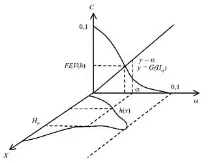
Ориз. 2. Графична интерпретация на размития интеграл
За да се опишат различни видове несигурност в теорията на размитите мерки, се използва общото понятие "степен на размиване". В общия случай включва "степен на важност", "степен на увереност" и, като отделен случай, "степен на членство" в теорията на размитите множества.Следователно една размита мярка може да се интерпретира по различни начини в зависимост от конкретното приложение.
Дефиницията на размито множество, което фиксира степента на членство на елемент xX в подмножествоAF(X),къдетоF(X)е множеството от всички размити подмножества на X, може да бъде представено с помощта на размит интеграл, както следва [3].
Нека е необходимо да се оцени степента на принадлежност на някакъв елемент към множеството. Очевидно е, че за празно множество тази степен на принадлежност е равна на 0, а за него е равна на 1, т.е. степента на членство за ще бъде по-голяма от тази за ако . Ако степента на принадлежност е равна наg(x0,E)и заедноEе дадено размито подмножество, тогава .
Това предполага, че степента на размиване на преценката „” е равна на степента на принадлежност към размитото подмножество. По този начин концепцията за степента на размиване в теорията на размитите мерки включва концепцията за степента на принадлежност към теорията на размитите множества.
За непрекъснато пространствоX=Rизчисляването на размития интеграл може да бъде опростено и намалено до намиране на стойността върху монограм (или таблица).
Нека е изпълнено условието:
xh(x)≥αi>=Fαi.
В случая е вярно следното. Акоf(x)е плътността на размитата мярка, стойността на размития интеграл наh(x)върху размитата мярка е равна на стойността , за която:
, , (6)
.
Дясната страна на (6) зависи само от стойноститеαиλи може да бъде получена предварително в цифрова форма под формата на таблица или графика. Лявата страна на (6) е съотношението на площта, дефинирана от набора от ниваHα,към цялата област на дефиниране на функцията за плътност на размитата мяркаf(x).
По този начин използването на (6) може да улесни организацията на изчислениеторазмит интеграл [1].
Като примери разгледайте изчисляването на размития интеграл за крайни множества в случаите наgλ- иgv-meep.
Нека е дадено множество от пет елементаX=i>, i. Всеки елементхiXсъответства на стойностите на размитите плътностиgiот Таблица 1.