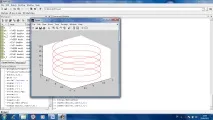
1 лекция Matlab (Интерфейс и операции в командния прозорец)

MATLAB Цел:е проектиран да извършва изчисления като

Най-простите изчисления с помощта на формули;

Решаване на нелинейни уравнения и системи;

Решаване на задачи по линейна алгебра;

Решаване на оптимизационни задачи;

Диференциация и интеграция;

Проблеми на обработката на експериментални данни (интерполация, апроксимация, метод на най-малките квадрати);

Решаване на обикновени диференциални уравнения и системи;

Решаване на диференциални уравнения в частни производни;

Освен това MATLAB предоставя широки възможности за създаване на графики (плоски и обемни).

MATLAB ви позволява да предоставите на своите програми визуален интерфейс.

Интерфейс:след стартиране се появява главният прозорец на приложението

Съдържа меню, лента с инструменти, работно пространство на командния прозорец, списък с последните команди в прозореца Хронология на командите, списък на файловете в работната папка в прозореца Текуща директория, които могат да бъдат заменени от прозорец на работното пространство, съдържащ списък с променливи, техния тип и стойност в текущия момент.

Командата на менюто на работния плот ви позволява да изберете разположението на прозорците

Оформлението на работния плот предлага набор от вече показани прозорци по подразбиране, както и други опции.

Операции вКомандаПрозорец:курсорът е позициониран след >> редът, съдържащ курсора, се нарича команден ред.

с напредването на работата текстът в прозореца се измества нагоре извън границитепрозорец. Но продължава. Можете отново да получите горния (долния) ред с текст в командния ред, като използвате стрелките нагоре (надолу).

Текстовата област над командния ред е само за копиране.

Когато въвеждате команди, те завършват с точка и запетая; в противен случай резултатите от изпълнението ще бъдат показани незабавно.

Ако не е предоставено име на променлива за резултата от изчислението, тогава името ans се присвоява по подразбиране.

Текущият документ, който отразява работата на потребителя и съдържа редове за вход, изход и съобщения за грешки, се нарича сесия. Стойностите на променливите, изчислени по време на сесия, се съхраняват в областта на паметта на работното пространство. Дефинициите на всички променливи и функции на дадена сесия могат да бъдат записани в .mat файл, но самата сесия не може да бъде запазена.

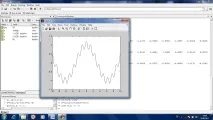
Нека начертаем функция на една променлива. За да направите това, задаваме диапазона от стойности за променливата x на аргумента на функцията. Нека x е масив от числа, първият му елемент е -10, последният му елемент е 10, стъпка 0.1 (т.е. всеки следващ елемент е по-голям от предходния с 0.1). За да направите това, въведете командата в командния ред

х=-10:0,1:10; След това получаваме стойностите на функцията y(x). За да направите това, в командния ред въведете командата y=cos(x/2)+cos(5*x)/5; След това в прозореца на работното пространство ще видите информацията, че x и y са масиви от числа и се състоят от 201 елемента всеки. Важно е броят на елементите в двата масива да е еднакъв. Тогава при изчертаване на графика числото от единия масив ще бъде хоризонталната координата на точката, а числото от другия масив ще бъде вертикалната координата на точката. Така графиката ще бъде изградена. Графична команда plot(x,y,'k-'); където първо се определя масив от координати по хоризонталната ос, след това по вертикалната ос и след това индикация за цвета на линията(k означава черно) и тип маркери ('k-' означава черна линия без маркери). Всички тези команди се виждат в прозореца Хронология на командите, където се записват.

Нека изградим няколко диаграми едновременно.

За да направите това, нека зададем масив x от -6,28 със стъпка от 0,1 до 6,28. х=-6,28:0,1:6,28; След това дефинираме функциите y(x), z(x), v(x). y=sin(x/2); z=cos(x); v=exp(cos(x)); След това въведете командата plot(x,y,'k-',x,z,'r.',x,v,'o-'); където всяка двойка (хоризонтални координати, вертикални координати) определя типа на маркера и цвета на линията. („r.“ червени точки без линия, „o-“ сини кръгове с линия).

Освен това командата grid on чертае решетка върху диаграмата, функцията title('Title') показва заглавието на диаграмата, функциите xlabel('Y-axis label'), ylabel('Y-axis label') се използват за етикетиране на осите.

нека изградим няколко графики отделно една от друга, но в един прозорец.

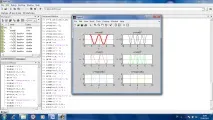
подзаговор (3,2,1); означава, че прозорецът е разделен на три малки прозореца за изчертаване вертикално, на две колони от такива прозорци хоризонтално и започваме да описваме първата (горе вляво) от графиките. По същия начин следващите команди за подграфа се различават само по номера на следващия график.

Когато се описват функции, съдържащи операциите умножение и степенуване, трябва да се има предвид, че техният аргумент е масив от числа. Съответно функцията също ще бъде получена като масив. Неговите елементи ще бъдат резултат от достъпа елемент по елемент на функцията до масива от аргументи. Затова в описанието на функцията y=cos(t).^2 се поставя знакът "точка"; или u=sin(t).^2; знакът за точка се поставя след аргумента, преди знака на операцията за степенуване.

Текстът (последователността от команди) се вижда в командния прозорец. Долната му част не се побираше, така че в прозореца История на командите се вижда катопродължение на текста, показан в командния прозорец, започвайки с командата plot(t,v,'c-');

нека начертаем графика в полярната координатна система. За да направим това, ние формираме масив от стойности на полярен ъгъл phi и полярен радиус ro и използваме командата polar(phi, ro, s), където s е низ от три знака, указващи цвета на линията, типа на маркера и типа на линията. Можете да се ограничите само до цвят и тип линия. MATLAB осигурява автоматична замяна на комбинации от латински букви с гръцки букви. Така например \phi се заменя с ϕ, \rho се заменя с ρ. Следователно в командата title('Title') ние посочваме в заглавието не гръцки букви, а съответните комбинации от латински букви.

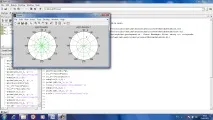
Нека изградим графика на функция, дадена в параметрична форма. За да направим това, дефинираме масив от параметъра t. След това дефинираме масиви от функции от параметъра. Нека x=f(t), y=g(t). След това начертаваме функцията y(x) с помощта на командата plot(x, y).

начертайте графика 2 x 3 -y 2 =0 (a>0). Параметричното представяне е: x=t 2 , y=at 3 , -∞ 2 +(x-a)y 2 =0, a>0. Параметричното представяне е: x(t)=a(t 2 -1)/(t 2 +1), y(t)=at(t 2 -1)/(t 2 +1)

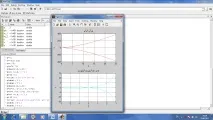
В MATLAB графиките могат да бъдат модифицирани с помощта на възможностите на графичния прозорец, в който се показват. За да направите това, използвайте инструмента със стрелка, за да маркирате елемент и след това щракнете върху бутоните на мишката, за да отворите съответните списъци с действия или елементи от менюто.

Командата File-Generate M-file ви позволява автоматично да генерирате файл с програма, която изгражда точно такава графика.

Можете да го запазите, като щракнете върху Запази.

Нека изградим триизмерна графика z(x,y). За да направите това, трябва да създадете двуизмерен масив за всяка от двете променливи x и y. Например x=-2:2 и y=-3: 3. Масивите се създават от командата

[x y]=meshgrid(-2:2, -3:3) по този начинформира решетка от координати в x и y.

След това изчисляваме за всяка точка с координати (x, y) стойността на функцията z (x, y), тоест координатите на тези точки по оста z.

z=y.^2-x.^2 След формирането на масива от координати по оста z, нека се обърнем към функцията mesh(x,y,z), която ще изгради повърхност, използвайки наличните координати.

освен това има и функция за изграждане на повърхност, оцветена според стойностите на z(x,y), тоест нещо като географска карта с оцветяване според височината на изобразения терен. Ние също така изграждаме мрежа за него с помощта на функцията meshgrid, след това намираме стойностите (масив от стойности) z(x,y) и след това извикваме surf(x,y,z).

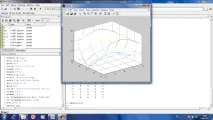
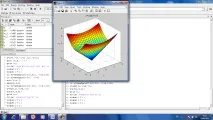
Триизмерна фигура може да се завърти на всяка страна и да се гледа по-удобно. За да направите това, в прозореца на фигурата трябва да натиснете бутона Rotate3D и можете да закачите и завъртите фигурата с мишката.

Ако трябва да изградите две 3D фигури в един и същи прозорец, тогава се използва командата задържане, която принуждава MATLAB да изгради нова 3D повърхност в същия прозорец.

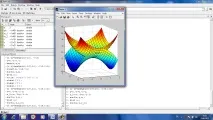
Нека построим повърхност, дадена параметрично.

Нека първо конструираме вектор колона u=(0:3.14/50:3.14)’ за параметъра u; знакът означава транспониране.

След това, за втория параметър v, конструираме вектор ред със същия брой (това е важно!) елементи v=(0:2*3.14/50:6.28);

Ние формираме матрица за x(u,v) като матрично произведение на колоната ch(u) и реда cos(v), т.е. x=cosh(u)*cos(v), където cosh е хиперболичен косинус на езика на операторите на MATLAB.

След това е необходимо да се формира матрицата z като матрично произведение на колоната sh(u) и низ от единици с еднаква дължина. За да изградите низ от единици с еднаква дължина, използвайте командата ones(size(v));

Така z=sinh(u)*ones(size(v));

тогава формираме графикаsurfacesurf(x,y,z);

Нека построим графика на движението на точка в равнина. Нека се движи по дадена параметрично крива. x(t)=cos(t), y(t)=3sin(t). Използваме оператора comet(x,y). Позволява ви да анимирате движението на точка.

Движението на точка по спирала, дадена параметрично x(t)=sin(t), y(t)=cos(t), z(t)=t, може да бъде симулирано с помощта на командата comet3(sin(t),cos(t),t);