10 парадокса, които ще ви изненадат KyKyRyzO
Парадоксът е твърдение, което очевидно си противоречи и все пак може да е вярно. Известно е, че повечето логически парадокси са невалидни аргументи, но те са ценни за развитието на критичното мислене. Ето десет парадокса, които силно ще ви изненадат.
1. Парадоксът на стойността: Защо водата е по-евтина от диамантите, когато хората се нуждаят от вода, а не от диаманти, за да оцелеят?
Парадоксът на стойността (известен също като парадокса на диаманта и водата) е очевидно противоречие: въпреки че водата е по-полезна по отношение на оцеляването, диамантите имат по-висока пазарна стойност. На ниво потребление водата има по-висока пределна полезност от диамантите и следователно е по-ценна. Хората обикновено консумират повече вода, отколкото диаманти, и следователно пределната полезност и цената на водата е по-ниска от тази на диамантите.
Обяснението на този парадокс гласи, че не общата стойност на диамантите или водата е важна, а стойността на всяка единица вода или диаманти. Вярно е, че полезността на водата за хората е огромна, защото те се нуждаят от нея, за да живеят. Въпреки това, тъй като водата е изобилна в света, пределната полезност на водата е ниска. С други думи, всяка допълнителна единица вода, която стане достъпна, може да бъде запазена за използване, когато е необходимо за оцеляване.
Следователно всяка единица вода губи стойност с увеличаване на количеството вода. От друга страна, диамантите се намират в по-малки количества. Те са в толкова малки количества, че стойността на един диамант е по-голяма от стойността на една чаша вода, която е налична в изобилие. Така диамантите са по-скъпи за хората. Затова желаещитедиамантите са готови да платят по-висока цена за един диамант, отколкото за една чаша вода, а продавачите на диаманти таксуват повече за един диамант, отколкото за една чаша вода.
2. Paradox на дядо: Какво ще стане, ако пътувате назад във времето и убиете дядо си, преди той да срещне баба ви?
Парадоксът на дядото е парадокс на пътуване във времето, описан от писателя на научна фантастика Рене Баржавел през 1943 г. в книгата му Le Voyageur Imprudent (Дървото на бъдещите времена).
Парадоксът е описан по следния начин: пътешественикът във времето се е върнал назад във времето, когато неговите баба и дядо още не са се оженили. По това време пътникът убива дядо си и следователно никога не се ражда. Ако той никога не се роди, тогава той не може да пътува назад във времето и да убие дядо си, което означава, че все пак ще се роди.
Ако приемем причинно-следствена връзка между настоящето и бъдещето на пътешественика във времето, парадоксът на дядото, който прекъсва тази връзка, може да се счита за невъзможен (като по този начин елиминира произволната промяна на съдбата). Има обаче много хипотези, които избягват парадокса, като идеята, че миналото е непроменливо, следователно дядото трябва вече да е оцелял след опита за убийство; или пътешественикът във времето създава допълнителен отрязък от време или паралелна вселена, в която пътешественикът никога не се ражда.
Вариант на парадокса на дядото е парадоксът на Хитлер или парадоксът на убийството на Хитлер, доста често срещан в научната фантастика, в който главният герой пътува във времето, за да убие Адолф Хитлер, преди да може да предизвика Втората световна война. Действие, предприето по време на пътуване във времето, премахва всяка причина за пътуването, заедно свсяко знание, че причината някога е съществувала, като по този начин се премахва всякаква нужда от пътуване във времето.
3. Парадоксът на Тезей: След като смените всички части на кораба, все още ли е същият кораб?
Корабът на Тезей е парадокс, който повдига въпроса дали обект, чиито компоненти са заменени, остава същият обект.
Парадоксът е обсъждан от древните философи и по-късно от Томас Хобс и Джон Лок. Някои казват "Обектът остава същият", а други казват "Обектът не остава същият".
Въз основа на тази теория има заключение, че това, което виждаме в огледалото, е напълно различно от това, което сме виждали преди седем или повече години, тъй като човешките клетки се възстановяват приблизително на всеки седем години.
4. Парадоксът на Галилей: Въпреки че не всички числа са квадратни, няма други числа освен квадратни.
Парадоксът на Галилей е демонстрация на едно от удивителните свойства на безкрайните числа. В последната си научна работа, Двете нови науки, Галилео прави противоречиви изявления относно положителните цели числа.
Първо, някои числа са квадратни, докато други не са; следователно всички числа, включително квадратни числа и неквадратни числа, трябва да са по-многобройни от квадратните числа. И все пак за всеки квадрат има едно положително число, което е неговият квадратен корен, и за всяко число има един квадрат; следователно не може да има повече от едното от другото. Галилей заключава, че тази идея се отнася за крайни множества, но не и за безкрайни множества.
През деветнадесети век, използвайки същите методи, немският математик Георг Кантор, който е най-известен като изобретателТеорията на множествата доказа, че това ограничение не е необходимо. Възможно е да се дефинират сравнения между безкрайни множества по смислен начин и че според това определение някои безкрайни множества са по-големи от други. Това продължава последната работа на Галилей върху безкрайните числа. Той показа, че броят на числата в линейния сегмент е същият като броят в по-големия линеен сегмент, но не откри доказателството на Кантор, че това е по-голямо от броя на целите числа.
5. Парадокс на спестяванията: ако всеки се опитва да спестява по време на рецесия, тогава съвкупното търсене ще спадне и общите спестявания на населението ще бъдат по-ниски.
Парадоксът на икономиите гласи, че ако всеки се опита да спести повече пари по време на икономическа рецесия, тогава съвкупното търсене ще спадне и на свой ред ще намали общите спестявания на населението поради намаляване на потреблението и икономическия растеж. Парадоксът твърди, че общите спестявания могат да намалеят, дори когато индивидуалните спестявания се повишат и като цяло увеличаването на спестяванията може да бъде лошо за икономиката, тъй като докато индивидуалното спестяване обикновено е добро за икономиката, колективното спестяване може да бъде лошо за икономиката като цяло. Хипотетично, ако всички хора спестяват парите си, спестяванията ще се увеличат, но макроикономическият статус ще намалее.
6. Парадоксът на Пинокио: Ами ако Пинокио каже „Сега носът ми расте“?
Парадоксът на Пинокио възниква, когато Пинокио казва „Носът ми сега расте“ и това е версия на парадокса на лъжеца.
Парадоксът на лъжеца се определя във философията и логиката като твърдението „Това изречение е невярно“. Всеки опит да се установи класическата степен на достоверност на това твърдение води до противоречие или парадокс. Това е така, защото ако твърдението „Това изречение е невярно“ е вярно, тогаваневярно е; това би означавало, че е технически вярно, но също така, че е невярно и така нататък до безкрайност.
Въпреки че парадоксът на Пинокио е част от парадокса на лъжеца, той е специален случай, защото няма семантични предикати, като например парадокса „Изречението ми е невярно“.
Парадоксът на Пинокио няма нищо общо с това, че Пинокио е известен лъжец. Ако Пинокио каже „Болен съм“, това може да е вярно или невярно изречение, но „Носът ми расте сега“ на Пинокио не може да бъде нито вярно, нито невярно; следователно тази и само тази фраза създава парадокса на Пинокио (лъжецът).
7. Парадоксът на бръснаря: В едно село, където бръснарят подстригва всички, които не подстригват косата си, кой подстригва косата на бръснаря?
Да речем, че минавате покрай бръснарница и виждате табела с надпис „Вие сами ли се подстригвате? В противен случай влезте и ще ви подстрижа! Ще подстрижа всеки, който не подстригва себе си и другите.“ Това изглежда достатъчно справедливо и сравнително просто, докато не дойде следващият въпрос в ума ви: "Бръснарят сам ли се подстригва? Ако го прави, не трябва, защото той не подстригва тези, които се подстригват, но ако не го прави, тогава трябва, защото той подстригва всеки човек, който не се подстригва." и т.н. И двете възможности водят до противоречие.
Това е парадоксът на бръснаря, който е въведен от британския математик и философ Бертран Ръсел в началото на ХХ век. Той разкри огромен проблем, който промени цялата посока на математиката от двадесети век.
В парадокса на бръснаря има условие „се подстригва“, но популацията от всички мъже, които сами се подстригват, не може да бъде събрана, въпреки че условието изглежда достатъчно просто, защото не можем да решим дали бръснарят трябва да бъде вагрегат или не. И двете условия водят до противоречие.
Опитите да се намерят начини за разрешаване на парадокса са фокусирани върху ограничаване на типовете множества. Самият Ръсел предложи "Теория на типовете", в която изреченията са построени йерархично. На най-ниското ниво изреченията са за хора. На следващото ниво изреченията са за компании от хора; на следващото ниво изречения за други компании от хора и т.н. Така се избягва необходимостта да се говори за множеството от всички множества, които не са членове на самите себе си, тъй като двете части на изречението са от различни видове - тоест те са на различни нива.
Поради тази и други причини най-предпочитаното решение на парадокса на Ръсел е така наречената теория на множествата Цермело-Френкел. Той ограничава предположението на теорията на множествата, което гласи, че при дадено условие винаги можете да направите набор, като съберете обекти, които отговарят на условието. Вместо това започвате с индивидуални условия, правите комплекти от тях и работите оттам. Това означава, че не трябва да приемате, че има набор от всички набори, не трябва да се опитвате да разделяте набори, които съдържат себе си, и тези, които не съдържат. Трябва само да можете да направите това разделяне за елементите на всеки даден набор, който сте създали от индивидуални условия в определен брой стъпки.
8. Парадоксът на рождения ден: Как двама души могат да споделят един и същи рожден ден в малка група?
9. Парадоксът на кокошката и яйцето: кое е първо, кокошката или яйцето?
Дилемата за причинно-следствената връзка кокошка-яйце обикновено е „Кое е първо, кокошката или яйцето?“; за древните философи въпросът за първенството на кокошката или яйцето повдигна и въпроси за това как се е появил животът и вселената като цяло.
Културният произход на кокошката и яйцето сочи безполезността на идентификациятапричина и следствие. Може да се счита, че в този подход се крие най-фундаменталният характер на въпроса. Буквалният отговор е очевиден за някои хора, яйцето идва преди пиленцето. За други на първо място е пилето. Метафоричното представяне обаче поставя метафизична дилема. За по-добро разбиране на неговия метафоричен смисъл въпросът може да се формулира по следния начин: „Кой беше първи, X, който не може да се появи без Y, или Y, който не може да се появи без X?“ Когато Земята беше създадена преди много години, беше създадено и пилето. Тогава тя снесе яйце. Ако яйцето беше първо, тогава кой трябваше да го излюпи и кой трябваше да го храни, когато стане пиленце?
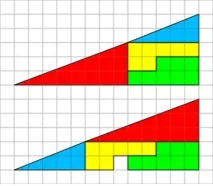
10. Парадоксът на пъзела с липсващия квадрат: Защо квадратът изчезна без причина?
Липсващият квадратен пъзел е оптична илюзия, използвана в часовете по математика, за да помогне на учениците да разберат геометричните фигури. Той изобразява две фигури, сглобени от едни и същи части в малко различни конфигурации.
Ключът към пъзела е фактът, че нито един от "триъгълниците" не е наистина триъгълник, защото хипотенузата е огъната. С други думи, "хипотенузата" не поддържа постоянен наклон, въпреки че може да изглежда правилна за човешкото око. И така, с хипотенузата, първата цифра всъщност заема 32 квадрата, докато втората заема 33, включително "липсващия" квадрат. Маркирайте точката, където се срещат червените и сините триъгълници в долното изображение (5 квадрата вдясно и две от долния ляв ъгъл) и сравнете със същата точка в другата фигура; ръбът е под знака в горното изображение, но се простира под него. Наслагването на хипотенузите на двете фигури създава много тънък успоредник с площ от една клетка -същата област "липсва" във втората фигура.