10 псевдослучайни кода (последователности)

Наред с ортогоналните кодове, важна роля в системите с разширен спектър играят псевдослучайните последователности, сред които най-важните са:

Формирането на M-последователността се осъществява от система от n-линейни регистри за съхранение на изместване и K суматори по 2, както и обратна връзка. Дължината на M-последователността се определя от броя на суматорите и може да бъде максимум , където:

n - брой регистри за съхранение на смени

Максималната постижима стойност на автокорелационната функция:

Помислете, като пример за формирането на M-последователността, система, състояща се от n \u003d 4 регистъра за съхранение на смени и k \u003d 1 суматори по 2:

Работата по генериране на M-последователността се извършва, както следва:

При всеки нов цикъл съдържанието на регистъра се измества с една позиция надясно.

Съдържанието на регистрите X3 и X4 се сумира с 2. Резултатът от сумирането се подава обратно към входния регистър X1. Крайната последователност е това. Какво се формира на изхода на регистър Х4

Нека регистрите съдържат следните двоични стойности:

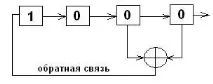
Тогава на изхода на регистъра X4 с всеки нов цикъл ще имаме:

Тъй като последното състояние на регистрите X1,X2,X3,X4 е идентично с оригиналното, заключаваме, че дължината на получената последователност е 15, което съответства на максималната възможна дължина:

Така на изхода на регистъра X4 получаваме двоична последователност от вида: 111101011001000.

Нека проверим тази последователност за произволност.

А) проверка за баланс

Количество "0"-7 изход:- балансиран

B) Проверка за цикличност:

Количествоцикли на "1" -4

Брой цикли от "0" -4

Освен това половината от тези цикли (т.е. 4) имат дължина =1

1/4 (т.е. 2) има дължина =2

Тъй като последователността е кратка по дължина, не е възможно да се провери допълнително, но е ясно, че условието за цикличност е изпълнено

В) Корелационен тест

Сравнете с оригинала

Това означава, че тази последователност е свързана

Тъй като всичките 3 условия са изпълнени, тогава тази последователност е псевдослучайна.

Ако анализираме този пример и схемата, показана на фигурата, е лесно да се види, че дължината, характеристиките и корелационните свойства на М-последователността значително ще зависят от броя на суматорите и формата на организация на обратната връзка. В този смисъл се разграничават "лоши" и "добри" М-последователности, отнасящи се до последните М-последователности с високи стойности на автокорелационната функция. По-нататъшно увеличаване на автокорелационната функция и постигането на добри кръстосани корелационни свойства между кодови последователности е възможно чрез комбиниране на няколко М-последователности. На този принцип се основават схемите за генериране на Gold кодове и Kassami кодове.

Те се формират на базата на 2 специално подбрани М-последователности и добавянето им символ по знак с 2. (вижте следващата фигура)

Съществен момент при формирането на Gold кодове е използването на специални двойки М-последователности, наречени предпочитани (изброени са в специалната литература)

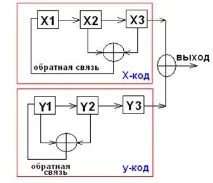
защото и двете M-последователности имат еднаква дължина M и се тактират от един генератор, тогава генерираната Gold последователност ще има дължина, равна на , където:

n е числотобитове от регистъра за смяна в генератора на единична последователност

Те се изпълняват с помощта на 3 последователно включени М-последователности, които също са избрани на базата на критерия за предпочитание с различни обратни връзки:

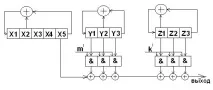
, където m 'и k' са циклични смени на кодове, генерирани съответно от регистри y и z

Генераторите на кодове за касови апарати с размери ( n (=5) m (=3) k (=3)), където n, m, k са броят на регистрите за съхранение на смени в генераторите на M-последователности x, y, z съответно, образуват кодови последователности с определени свойства само ако y и z M-последователностите имат различни спрямо една друга циклични смени, дадени от m ' и k '

Семейството от кодове на Касами съдържа последователности с период

Те се считат за оптимални в смисъл, че за всяка двойка кодови последователности на Касами максималните стойности на автокорелационната функция са равни на: