13.2. Метод на спомагателна режеща равнина
Този метод се използва за изграждане на линия на пресичане на две повърхности, когато секущите (успоредни) равнини, когато се пресичат с тези повърхности, образуват прости линии (права линия или кръг).
13.2.1Задание:са дадени повърхнините на конус

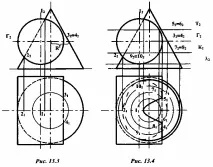
Решение:оста на цилиндъра е перпендикулярна на равнинатаP2,следователно повърхността на цилиндъра е проективна. В този случай проблемът може да бъде решен по същия начин, както беше анализиран в предишния (раздел 13.1.1) пример. За целта се определят референтни точки - най-високата и най-ниската точка 1 и 2, които лежат в пресечната точка на челната проекция на цилиндъра с образната на скицата на конуса. Техните хоризонтални проекции 11 и 21 принадлежат към хоризонталната проекция на образната на скицата на конуса (l1 и 21, съвпадат с аксиалната линия на конуса). Точки 3 и 4 определят видимостта на пресечните линии върху хоризонталната проекция. За определяне на техните хоризонтални проекции през оста на цилиндъра, успоредна наP1, се начертава спомагателна секуща равнина Г (челната й следа Г2). Тази равнина ще изреже цилиндъра по протежение на образуващите очертания, а конуса по дължината на окръжността с радиус R, която ще бъде проектирана върху P1 в пълен размер. Пресечната точка на този кръг с генераторите на очертанията на цилиндъра не е нищо друго освен хоризонталните проекции на референтни точки 31 до 41 (фиг. 13.3).
Конструкцията на междинните точки е подобна на конструкцията на точки 3 и 4, само генераторите, по които спомагателната равнина ще реже цилиндъра, няма да бъдат схематични (фиг. 13.4).
13.3. Метод на спомагателните концентрични сфери
Този метод се използва за начертаване на пресечна линия на две повърхности на въртене, когато техните оси се пресичат и са успоредни.проекционна равнина. Пресечната точка на осите се приема за център на спомагателните концентрични секущи сфери.
13.3.1Задача:Дадени са две повърхности на въртене - конус и цилиндър, чиито оси се пресичат и са в една равнина, успоредна наП2(фиг. 13.5). Необходимо е да се начертае линия на тяхното пресичане.
Решение:на фронталната проекция фиксирайте пресечните точки на меридианите на дадените повърхности на оборот 12 и 22 - те принадлежат на желаната пресечна линия. Хоризонталните проекции на тези точки са върху аксиалната линия на конуса и цилиндъра - 1, и 2,. Други точки на пресечната линия могат да бъдат конструирани с помощта на концентрични сферични медиатори като спомагателни секущи повърхности. От точката на пресичане на осите на фронталните проекции, както от центъра, се изчертават сфери. Първият е допирателен към проекцията на конуса, а следващите имат голям радиус (фиг. 13.6).
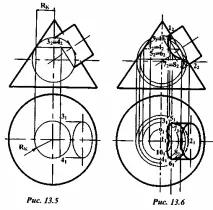
Всяка сфера пресича двете повърхности по окръжности, чиито фронтални проекции са изобразени като прави сегменти. Тези проекции се пресичат в точки, които са фронтални проекции на точките от необходимата линия на пресичане на повърхнините.
Хоризонталните проекции на тези точки се определят от принадлежността към една от повърхностите. В този случай е по-удобно да ги получите, като принадлежите към конуса. Например, точки 3 и 4 лежат на същата окръжност, по която спомагателната сфера пресича конуса. Променяйки радиуса на спомагателната секуща сфера, те намират последователна поредица от точки на пресечната линия, свързвайки които, получават проекциите на желаната линия (фиг. 13.6). За да се определи видимостта на хоризонталната проекция на пресечната линия, на нейната челна проекция се отбелязват точки, които лежат на аксиалната линия на цилиндъра и принадлежат на пресечната линия. След това по линиите на проекциятавръзките ги прехвърлят към генераторите на контури на хоризонталната проекция на цилиндъра. Точките под посочените ще бъдат върху невидимата част на цилиндъра.