1.5.2 Интервална оценка на резултатите от измерването

При голям брой тестове точковите оценки на индикаторите ще се доближат до истинските стойности, но е трудно да се направят наистина голям брой тестове. Следователно в този случай се използват интервални оценки, чиято надеждност се характеризира с доверителна вероятност за резултата от измерването. Използването на интервални оценки дава възможност да се свържат показателите за точност и надеждност с броя на опитите.

За да се установи такава връзка, е необходимо да се определи точното разпределение на характеристиката на извадката (статистическа оценка) въз основа на вида на закона за разпределение на генералната съвкупност (резултат от измерването). Следователно, в процеса на получаване на оценки на интервалните измервания, последователно се решават четири задачи:

проверка на съответствието на резултатите от измерването с нормалния закон за разпределение (или неговото приемане)

изчисляване на доверителните граници за очакваната стойност на резултата от измерването

изчисляване на доверителни интервали за стандартното отклонение на резултата от измерването

откриване на груби грешки (пропуски).

Нормален закон за разпределение на вероятностите при измервания.

В процеса на оперативни наблюдения резултатът от измерването на параметъраХна системата се влияе от голям брой различни по природа фактори. Това води до вероятностния характер на измерената стойност. В този случай се приема хипотезата за нормалния закон за разпределение на резултатите от измерването на параметъра. Широкото разпространение на нормалното разпределение на грешките в измервателната практика се обяснявас централната гранична теоремана теорията на вероятностите, която е една от най-забележителните математически теореми, в чието разработване са участвали много математици - De Moivre, Laplace, Gauss, P.L. Чебишев, А.М. Ляпунов.

Централнаграничната теорема казва, че разпределението на случайните грешки ще бъде близко до нормалния закон, когато резултатите от измерването се формират под въздействието на голям брой независимо действащи фактори, всеки от които има само малък ефект в сравнение с общия ефект на всички останали. Ето защо при измерванията обикновено се приема хипотезата за нормално разпределение на грешките при измерване.

Тоест, измереният параметърXима нормално разпределение със средно (очакване)

и дисперсияσ2:

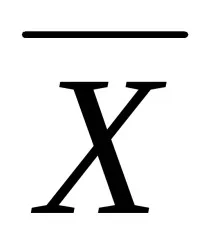
. 1.6

Очевидно, тъй като дисперсията (стандартното отклонение на измерването) се увеличава, разпределениетоf(x)се разпространява. Това води до факта, че вероятността от поява на големи грешки се увеличава, а вероятността от поява на по-малки грешки намалява, т.е. разсейването на резултатите от измерването се увеличава.

Функцията на Гаус има формата на камбана, като максимумът на функцията се достига в точка

, а самият максимум е . На практика резултатът S трябва да се използва вместо .

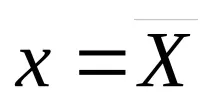
Законът за нормалното разпределение на плътността на вероятността съответства на интегралната функция на разпределение на Лаплас от формата:

---