§ 2. Основни свойства на поляризираните фотони
Поляризираната светлина може да бъде получена чрез преминаване на обикновен светлинен лъч през някакво поляризиращо устройство, като полароиден филтър или калцитен кристал - двупречупваща призма. Поляризационната ос на лъча се определя от ориентацията на оптичната ос на призмата, така че на изхода на оптичното устройство (призма) се получават два лъча - с посока на поляризация (директен лъч) и с перпендикулярна посока +90 0 (ортогонален лъч). Най-общо казано, може да се приеме, че единични поляризирани фотони също могат да бъдат генерирани чрез отделянето им от поляризиран светлинен лъч, въпреки че това може да не е технологично осъществимо. В следващия раздел приемаме за простота, че такива единични фотони с определени посоки на поляризация вече съществуват, но след това в § 4 показваме как това предположение може да бъде елиминирано.
Въпреки факта, че посоката на поляризацията е непрекъсната величина, принципът на несигурността на Хайзенберг не позволява такова измерване на състоянието на всеки отделен фотон, което би разкрило повече от един бит информация (във вероятностен смисъл) за неговия поляризационен ъгъл.
Например, ако светлинен лъч с поляризационна ос, насочена под ъгъл , падне върху двупречупваща призма с ъгъл на оптичната ос , тогава всички отделни фотони се държат по дихотомичен и напълно непредсказуем начин, появявайки се на изхода на призмата в директния лъч с вероятност cos 2 (-) и съответно в ортогонален лъч с вероятност sin 2 (-), поляризаторът в същото време съответно под ъгъл и +90 0 . Детерминистично, всички фотони се държат само когато двата водача са или успоредни един на друг (= и тогава всички фотони се появяват в директния лъч) или перпендикулярни ( и в този случай всички фотони се появяват в ортогоналния лъч).(Приложение, стр. 1)
В случай, че осите не са перпендикулярни една на друга, има надежда, че може да се намери допълнителна информация за , като се направят многократни измервания за фотони в директния и ортогонален лъч с помощта на някакъв вид поляризатор, който ще бъде ориентиран под някакъв трети ъгъл. Подобно измерване обаче се оказва напълно безполезно, тъй като всички фотони, които се появяват в директен или ортогонален лъч, се оказват поляризирани точно под ъгъл или +90 0 , като същевременно губят всякаква информация за предишната си поляризация под ъгъл . Разбира се, ако е известно, че лъчът се състои от няколко еднакво поляризирани фотона, тогава, за да се получи повече от един бит информация относно техния общ поляризационен ъгъл, могат да се направят различни измервания за различни фотони.
С други думи, човек може да се надява да научи повече от един бит информация за един фотон, без директно да измерва поляризационния му ъгъл, а по-скоро по един или друг начин да разшири (клонира) един фотон към ансамбъл от еднакво поляризирани фотони, за да извърши впоследствие различни измервания върху тях. Тази надежда обаче също се оказва напразна, тъй като съществуването на такъв ансамбъл, както може да се покаже, не е в съответствие с основните положения на квантовата механика, а именно с линейността на трансформациите върху векторите на определено хилбертово пространство, което е набор от квантови състояния [9].
Формално в квантовата механика вътрешното състояние на квантовата система (като поляризацията на фотон) се представя като вектор с единична дължина в линейно пространство над полето от комплексни числа, тоест в така нареченото Хилбертово пространство. Размерността на това Хилбертово пространство зависиот самата система и може да бъде доста голям (или дори безкраен) за по-сложни системи.
Всяко физическо измерване, което може да се извърши в системата, съответства на някакво разлагане на хилбертовото пространство на ортогонални подпространства, всяко от които съответства на един от възможните резултати от това измерване, възникващи с една или друга вероятност. По този начин броят на възможните резултати от измерване (елементарни резултати от съответната вероятностна схема) е ограничен от размерността d на разглежданото Хилбертово пространство. Най-пълните измерения са тези, които съответстват на разлагането на хилбертово пространство на d едномерни подпространства.
Хилбертовото пространство за единичен поляризиран фотон е двумерно. По този начин състоянието на фотона може да бъде напълно описано като линейна комбинация, например, от два единични вектора r1=(1,0) и r2=(0,1), представляващи съответно хоризонталната и вертикалната поляризация. По-специално, фотон, поляризиран под ъгъл спрямо хоризонталата, се описва от вектора на състоянието (cos, sin). В случай, когато такъв фотон се измерва за хоризонтална или вертикална поляризация, той всъщност избира дали да стане хоризонтално поляризиран с вероятност cos 2 и вертикално поляризиран с вероятност sin 2 , че двойката вектори (r1, r2) съставляваправоъгълната основана разглежданото Хилбертово пространство.
Друга възможна основа за същото хилбертово пространство е дадена от два диагонални вектора
d1=

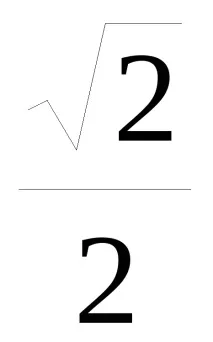
В тазидиагонална основаd1 представлява 45° поляризиран фотон и d2 представлява 135° поляризиран фотон.
Две бази се наричат спрегнати, ако всеки вектор от една база има проекции с еднаква дължина върху всички вектори от другата база. Това, разбира се, са правоъгълната и диагоналната основа. Равенството на проекциите означава, че система, подготвена като един от векторите в една от тези бази, ще се държи напълно непредвидимо и ще загуби цялата информация за себе си, отразена в тази база, след като бъде подложена на измерване, което съответства на друга база.
От практическа гледна точка е достатъчно да се разбере само, че има две прости устройства. Единият от тези инструменти може детерминистично да разграничава хоризонтално поляризирани и вертикално поляризирани фотони, а другият може детерминистично да разграничава фотони с различна диагонална поляризация - 45° и 135°. Ако обаче първото устройство се използва за определяне на състоянието на диагонално поляризиран фотон (а второто - за правоъгълно поляризиран), тогава в такава ситуация фотонът ще се държи по напълно случаен и непредсказуем начин и такова измерване няма да позволи изобщо да се определи поляризационният му ъгъл. Във вероятностен смисъл, с такова измерване, и двете поляризационни стойности стават еднакво вероятни.