2.2. частична графика
За графG=, графH= се наричачастиченграфик на графикG, ако съдържаU’нU. Имайте предвид, че частичният граф е даденна всички върховена оригиналния график.
ГрафP= се наричаподграфна графG, акоA'nAиU''е подмножество от всички дъги отU, дефинирани върху върхове отА'.
Ако в графиката на фиг. 2.1 премахнем, например, дъгите (3,5) и (2,1) от множеството от нейните дъги, тогава ще получим частична графика на оригиналната графика. Ако премахнем, например, връх 5 и всички дъги, свързани с него (дъги (5,2), (5,4) и (3,5)), тогава получаваме подграф на оригиналния график. И накрая, ако премахнем, например, дъгите (3,2) и (2,1) от получения подграф, получаваме пример за частичен подграф.
2.3. Неориентирани графи
Графът се наричанеориентиранилинедиграф, ако елементите на множествотоUв него се считат за неподредени, т.е. в него двойката(ai,aj)е неразличима от двойката(aj,ai).В този случай елементите на множествотоUсе наричат ръбовеи на фигурата те са показани като cur пет сегмента без стрелки.
Аналогът на пътя в недиграф е понятиетоверига. Веригата може да бъде проста или съставна, елементарна или не. Затворената верига се наричацикъли се въвежда подобно на понятиетоконтур.
Всеки диграф е уникално свързан с не-диграф, ако всички дъги са заменени с ръбове, т.е. премахнете ориентацията. Ако диграфът има двойки дъги, свързващи едни и същи върхове в противоположна посока, тогава те се заменят с единичен ръб. И така, недиграфът, свързан с графа, даден в примера, ще има броя на ребра с едно по-малък от броя на дъгите, тъй като двойката дъги (1,2) и (2,1) ще бъде свързана с еднаръб, край.
Терминътверигаможе също да бъде въведен за насочен граф, означаващ под него последователност от дъги без оглед на ориентацията. Така че в нашия пример можем да говорим за веригата (1,2,5,4).
Един граф се наричасвързан, ако всяка двойка върхове в него е свързана с верига.
Свързаният компонентна граф е неговият свързан подграф, за който няма друг свързан подграф, който да включва дадения като свой подграф.
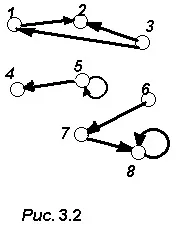
По този начин, свързан компонент е максимален свързан подграф в граф. Фигура 2.2 показва граф с три свързани компонента: подграфи във върховете , , .
Сега можем да кажем, че графът е свързан, ако съдържа само един свързан компонент.
Ръб на графика, чието премахване увеличава броя на свързаните компоненти, се наричамостилипровлак. В нашия пример един от мостовете ще бъде ръбът (6,7).
2.4. Разширения на модела
Графичният модел може да бъде разширен, когато се описват конкретни обекти, процеси или явления. За да направите това, използвайте следните методи:
- Дъги за претегляне (ребра). На всяко ребро (дъга) на графиката е присвоено число - теглото на дъгата (ръба). Теглото може да определи например разстоянието между градовете, ако върховете са присвоени имената на градовете, а ръбовете са пътищата между тях. За да се опише претеглена графика, се използва матрица на съседство, в клетките на която са записани теглата.
- Претегляне на върхове. Подобно на дъгите, теглата се присвояват на върховете. Например върховете представляват магазини и складове, а теглото на върха определя количеството на даден продукт в склад или магазин.
- Претегляне на дъги и/или върхове чрез вектори. Претеглянето се извършва не чрез число, а чрез набор от числа. Например за път, разстояние, тарифа, времепо пътя и т.н.
- В един граф са разрешени няколко "успоредни" дъги (или ръбове) между два върха. В този случай говорим за множество дъги (ръбове) и такива графи се наричат мултиграфи. За описване на мултиграфи се използват същите таблици като за прости графики, но в клетките не се записват 0 и 1, а кратността на дъгата.
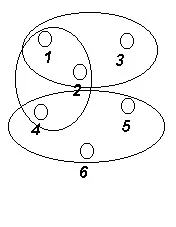
- Графиката използва не двоична, аr-арна релация, къдетоr> 2. Такива графики се наричат хиперграфи. За да се представят тези графики в равнина, върховете, които принадлежат на едно и също ребро, са свързани чрез затворени линии, както на фиг. 2.3. Тук графиката има три ребра: (1, 2, 3), (1, 2, 4), (4, 5, 6). Такива графики се появяват при описване на логически мрежи, когато елементите са във връзка, ако имат полюси, свързани с обща верига.