2.26Четириполюсници

Четири извода е електрическа верига, която има два входа и два изхода (трансформатор, електропровод, усилвател и др.).

Графично четириполюсникът обикновено се изобразява като правоъгълник с краища (полюси), излизащи от него, както е показано на фигура 2.44.

Фигура 2.44– Четириполюсник

Ако вътре в четириполюса има източници на електрическа енергия, той е активен, а буквата"А"е поставена вътре в правоъгълника.

Четириполюсът е преносна връзка между източника и товара. В този случай обект на изследване са токовете и напреженията на изводите на четириполюсника, а не вътре в него. Изводитеmn, към които е свързан източникът, се наричат ​​входни, а изводитеpq, към които е свързан товарът, се наричат ​​изходни.

Четириполюсниците могат да бъдат класифицирани според различни критерии:

1. по характера на съставните елементи -линейни инелинейни ;
2. според схемата на вътрешните връзки -Г-образна; Т-образна; U-образна и др.
3. прави разлика междусиметрични и асиметрични четириполюсници.

Четириполюсникът е симетричен, когато размяната на неговите входни и изходни клеми не променя токовете и напреженията във веригата, към която е свързан.

Основното значение на теорията на квадриполите е, че с помощта на някои обобщени параметри на квадрипол е възможно да се намерят токове и напрежения на неговия вход и изход.

Всяка сложна електрическа верига може да бъде представена като набор от сложни четириполюсници, свързани по определена схема.

За всеки пасивен четириполюсник напрежението и токът на входаÚ1Í1са свързани с напрежението и тока на изходаÚ2Í2уравнения:

В тези уравнения комплексните коефициентиA, B, C, Dзависят от веригата на вътрешните връзки на четиритерминалната мрежа, от стойностите на съпротивлението на веригата и от честотата. За всеки четириполюс те могат да се определят чрез изчисление или емпирично.

Коефициентите са свързани със съотношението:

Получаваме уравнения 13.1. За тази цел свързваме източника на ЕМП към клемите mn и товараZ2към клемитеpq(фиг. 2.45, а).

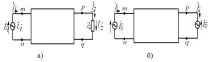
Фигура 2.45- Четириполюсник с източник на ЕМП и товар

Товарно напрежение. Използваме компенсационната теорема и заместваме съпротивлението на натоварванеZ2с източник на ЕМПÉ2, насочен към токаН2и числено равен наÚ2(фиг. 2.45,b).

Нека напишем изрази за токовеН1иН2презÉ1иÉ2и входна и взаимна проводимост.

EMFÉ1е насочена според токаÍ1, така че ще влезе в уравнението със знак плюс; ЕМПÉ2е насочена противоположно на токаН2и следователно влиза в уравнението със знак минус.

Като се има предвид, чеY12=Y21, от уравнение (2.102)

Замествайки (2.103) в (2.101), получаваме:

Ако входните и изходните клеми са разменени, уравненията ще бъдат подобни:

и константитеA', B', C', D'се определят от израз (2.105), ако индексите1и2са разменени.

Следователно уравненията на четириполюсник, захранван от изходната страна, ще бъдат:

т.е. техните коефициенти се различават по това, че константитеAиDса обърнати.

От това следва, че в симетричен четириполюсA=D.

С помощта на уравненията на четириполюса е възможно да се определи режимът на натоварване, т.е. намеретеÍ1иÚ1дадениÍ2иÚ2.

---