2.5.3. Метод на моментите
Методът е предложен от К. Пиърсън през 1894 г. Същността на метода:
избират се толкова емпирични моменти, колкото са необходими за оценка на неизвестните параметри на разпределението. Желателно е да се използват моменти от по-нисък порядък, тъй като грешките при изчисляването на оценките се увеличават рязко с увеличаване на реда на момента;
моментните оценки, изчислени от DE, се приравняват към теоретичните моменти;
параметрите на разпределението се определят по отношение на моментите и се съставят уравнения, изразяващи зависимостта на параметрите от моментите, което води до система от уравнения. Решението на тази система дава оценки на параметрите на разпределението на генералната съвкупност.
Пример 2.4.Да приемем, че случайната променливаXима гама разпределение. Необходимо е да се намерят оценки за параметрите на това разпределение (може да се отбележи, че нормалното разпределение е частен случай на гама разпределението).
Решение.Функцията на плътност на гама разпределението има формата
Разпределението се характеризира с два параметъраνи λ, така че единият параметър трябва да се изрази чрез оценката на математическото очакване, а другият - чрез оценката на дисперсията. Математическото очакване и дисперсията на това разпределение са съответноν/λ иν/λ2. Нека техните оценки са дефинирани равни:
Нека съставим система от уравнения за оценените параметри
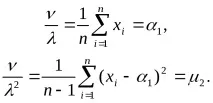
Разделяйки оценката на математическото очакване на оценката на дисперсията, получаваме
Методът на моментите позволява да се получат последователни, достатъчни оценки; при доста общи условия те са асимптотично нормално разпределени. Промяната може да бъде елиминирана чрез въвеждане на корекции. Ефективността на оценката е ниска; дори при големи размери на извадката, дисперсията на оценките е относително голяма (с изключение на нормалното разпределение, за коетометодът на моментите дава ефективни оценки). При изпълнение методът на моментите е по-прост от метода на максималната вероятност. Спомнете си, че е целесъобразно да се използва методът за оценка на не повече от четири параметъра, тъй като точността на пробните моменти рязко намалява с увеличаване на техния ред.
2.5.4. Квантилен метод
Същността на квантилния метод е подобна на метода на моментите: избират се толкова квантили, колкото е необходимо за оценка на параметрите; неизвестните теоретични квантили, изразени чрез параметри на разпределение, се приравняват на емпирични квантили. Решението на получената система от уравнения дава необходимите оценки на параметрите.
ДисперсиятаD(xG)на квантила на пробата е обратно пропорционална на квадрата на плътността на разпределение
в близост до точкатаxG. Следователно, квантилите трябва да бъдат избрани близо до тези стойностиx, в които плътността на вероятността е максимална.
Пример 2.5. Оценете параметрите на нормалното разпределение на случайна променлива, като използвате метода на квантилите.
Решение.Тъй като се изисква да се определят два параметъра на разпределениеmиS,, ще изберем два емпирични квантила от серията вариации. Например, можете да вземете
Използвайки стандартните функции на математическите пакети, за избраните стойностиG1иG2, ние определяме стойностите на аргументите на функцията на теоретичното разпределение за стандартизираната променлива
Съставяме система от две уравнения
Решението на системата ще ни позволи да намерим необходимите оценки на параметрите
Квантилният метод дава възможност да се получат асимптотично нормални оценки, но те носят известна субективност, свързана с относително произволен избор на квантили. Ефективността на оценките не е по-висока от метода на моментите. Дефинирането на прогнози може да доведе до необходимостта от численирешаване на доста сложни системи от уравнения.
Оценките, изчислени на базата на различни методи, се различават. Няма универсален отговор на въпроса кой от разгледаните методи е по-добър и дали трябва да се разчита на този метод за решаване на всеки проблем. Стойността на оценката във всеки отделен случай (за различни проби) се различава от истинската стойност на параметъра с неизвестна сума, с други думи, има известна несигурност при познаването на действителната стойност на параметъра. Качеството на оценките може да се определи индиректно чрез проверка на съответствието на емпиричните данни и теоретичния закон за разпределение.