26 март 2013 г

§19. Графика като линейно картографиране и линеен оператор

Дефиницията на булево (множество от подмножества) на произволно крайно множество от структурата на векторно пространство по отношение на операциите на добавяне на пръстен (сума на пръстена) и умножение на булеви елементи по числа от $GF(2)$ направи възможно въвеждането на векторното пространство $W_$ в теорията на графите. Спомнете си, че това е $m$-измерно векторно пространство върху булевото на $R$ набора от ръбове на $(n,m)$-графа $\Gamma (V,R)$. Очевидно никой не ни пречи да въведем в разглеждане подобно $n$-мерно векторно пространство $W_$ върху булевата стойност на набора от върхове $V$ на същия график. Ясно е, че въвеждането на ново понятие трябва да бъде оправдано с нещо. По този начин въвеждането на пространството $W_$ е оправдано от наличието в това пространство на две подпространства $W_C$ (цикли) и $W_S$ (разфасовки) — две подпространства, които имат различна графична интерпретация. Как може да се оправдае въвеждането на пространството $W_$? Въвеждането на пространството $W_$, заедно с наличието на пространството $W_$, ни позволява да хвърлим нов поглед върху графиката, а именно да дефинираме графика като линейно преобразуване на пространството $W_$ в пространството $W_$, преобразувайки всеки ръб към неговите два крайни върха. Известно е, че преходът от векторни пространства към съответните координатни пространства, изоморфни на тях, позволява да се определи линейно преобразуване чрез неговата матрица, което зависи от избора на основите на пространствата (преобразуваното пространство и пространството, в което се извършва преобразуването). Няма нищо изненадващо във факта, че графиката като линейно картографиране в "каноничните" бази на булевите стойности на множеството от ребра и множеството от върхове съответства на матрицата на инцидентност на графиката. (Под каноничния базис на векторното пространство на булевото на множеството $M = \$ имаме предвид базиса, съставен от елементите на същото множество,тези. основа $\)$.

Припомнете си как се конструира матрицата $B$ на линейното преобразуване $\Re$ от векторното пространство $L_1$ към векторното пространство $L_2$. Линейното картографиране $\Re$ се прилага към $j$-тия базисен вектор на картографираното пространство. Образът на това преобразуване, като вектор на пространството $L_2$, се разлага според основата на това пространство. В $j$-тата колона на матрицата $B$ са записани коефициентите (координатите) на разлагането на образа на $j$-тия базисен вектор на пространството $L_1$ в базиса на пространството $L_2$. Така матрицата $B$ има размерността $\dim L_2 \times \dim L_1$ (броят на редовете на матрицата е равен на размерността на пространството $L_2$, а броят на колоните е размерността на пространството $L_1$).

Ако вземем пространството $W_$ с неговата канонична основа като линейното пространство $L_1$, пространството $W_$ с неговата канонична основа като линейното преобразуване $\Re$, $(n,m)$-графа $\Gamma (V,R)$ като линейно преобразуване $\Re$, тогава (0,1)-матрицата $B$, с размерност $n\times m$, на графиката $\Gamma$, ще наистина е матрицата на инцидентност на тази графика като линеен дисплей.

В координатните пространства $W_$ и $W_$ операцията за преобразуване на елемент (координатна колона) $X \in W_$ в някакъв елемент $Y \in W_$ се свежда до умножаване на матрицата $B$ по колоната $X$, т.е. намалява до $BX = Y$.

Спомнете си, че изразът $BX = Y$, с известен $Y$, нарекохме "графично уравнение", което има решение само ако $Y$ принадлежи на подпространството от изображения на преобразуването, дадено от матрицата $B$.

От теорията на линейните преобразувания е известно, че множеството $L \subset W_$ от вектори $X \in L$, които са преобразувани от матрицата $B$ на нула в пространството $W_$, наречено ядро на линейното преобразуване, дадено от матрицата $B$, е подпространство на координатното пространство $W_$.Тъй като ядрото на това преобразуване съвпада с пространството на решенията на хомогенното графово уравнение $BX = 0$, което съвпада с пространството на графовите цикли, тогава $L = W_C$. Тоест, подпространството от цикли $W_C$ е ядрото на графиката $\Gamma (V,R)$, разглеждана като линейно преобразуване на пространството $W_$ в $W_$. Тази забележка позволява да се намерят фундаментални цикли като елементи на фундаменталната система от решения на уравнението $BX = 0$.

Бележка 1. Като се вземе предвид ортогоналността на подпространствата $W_C$ и $W_S$ над полето $GF(2)$, както и формата на матрицата $F$ от раздел 18, е лесно да се организира изчислителна процедура за конструиране на фундаментална система от разфасовки, „консистентна“ (чрез един и същи скелет) с всяка конкретна фундаментална система от цикли.

И така, по-горе отбелязахме важността на въвеждането на пространството $W_$, за да дефинираме графика като линейно преобразуване на пространството $W_$ в пространството $W_$. Но никой не си прави труда да разглежда графиката като линеен оператор, действащ от пространството $W_$ в себе си, преобразувайки всеки връх в неговия "окол" (множеството от върхове, съседни на него). Ако изберем каноничен базис в пространството $W_$, то в координатното пространство $W_$ графът $\Gamma $, като линеен оператор, който ще бъде означен с $\bf$, ще съответства на матрицата на съседство $A$ на графа.

Тъй като всяко решение на уравнението $AX = 0$ е линейна комбинация върху $GF(2)$ от решенията на фундаменталната система на това уравнение, ще започнем с конструирането и тълкуването на решенията на фундаменталната система. Означаваме с $X_1, X_2, . X_k$, където $k = n - ранг A$ ($n$ е редът на матрицата $A$, а $rank A$ е рангът на матрицата $A$) фундаменталната система от решения на уравнението $AX = 0$. Тъй като всяко решение $X_j$ $(j = 1,2. k)$ е елемент от $\ker A$ (ядрото на оператора $\bf$),тогава за това решение всичко, което беше казано по-горе относно произволен елемент от ядрото, трябва да бъде изпълнено. Разбира се, има някои особености на решението $X_j$, свързани с особеностите на процеса на конструиране на фундаменталната система от решения на уравнението $AX = 0$, но за идентифицирането им са необходими допълнителни изследвания.

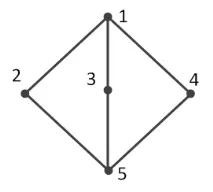
Нека илюстрираме казаното с примери за графики, дадени на фигури 1а и 1б.


Ориз. 1а	Ориз. 1б

За графиката от Фигура 1a, матрицата на съседство $A$, фундаменталната система от решения $X_1, X_2, . X_k$ на уравнението $AX = 0$, останалите нетривиални решения на това уравнение ще бъдат следните:

$ A = \left( 0 & 1 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & 1 & ; ; 0 \\ \end >> \right)$, $X_1 = \left( 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ \end >> \right)$, $X_2 = \left( 0 \\ 1 \\ 0 \\ 1 \\ 0 \\ \end >> \right)$, $X_3 = \left( 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ \end >> \right)$, $X_1 + X_2 = \left( 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ \end >> \right)$, $X_1 + X_3 = \left( 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ \end >> дясно)$, $X_1 + X_3 = \left( 1 \\ 1 \\ 1 \\ 0 \\ 1 \\ \end >> \right)$ $, $X_2 + X_3 = \left( 1 \\ 1 \\ 0 \\ 1 \\ 1 \\ \end >> \right)$, $X_1 + X_2 + X_3 = \left( 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ \end >> \right)$.

Подграфите, генерирани от тези решения, са показани на фигура 2.

Подграфите, генерирани от тези решения, са показани на фигура 3.

Нека обобщим резултатите от анализирания пример. За да направим това, ние въвеждаме в разглеждане матрицата $\bar = \left( \right)^T$, конструирана от колоните на фундаменталната система от решения на уравнението $AX = 0$, където $A$ е матрицата на съседство на някакъв $n$-върхов график, итранспониран. Матрицата $\bar $ ще има размерност $k\times n$ и $rank \bar = k$. Разгледайте матричното уравнение (система от уравнения) $\bar Y = 0$. Означаваме с $Y_1, Y_2, . Y_$ фундаменталната система от решения на това уравнение. Очевидно тези решения ще бъдат ортогонални на колоните $X_1, X_2, . X_k$ (следва от равенствата $\bar Y_j = 0$ за $j = 1,2. n - k)$ и ще формира основата на ортогонално подпространство към ядрото на оператора на графиката в координатното пространство. Означаваме (за аналогия с раздел 18) с F матрицата $F = \left( , X_1, X_2, . X_k> \right)$. Тогава отвореният въпрос, формулиран по-горе, ще звучи така: докажете или опровергайте твърдението, че уравнението $FZ = I$ е винаги разрешимо върху $GF(2)$ ($I = \left( \right)^T$). Това означава, че всяка графика може да бъде представена като пръстеновидна сума на някои подграфи, генерирани от колоните $Y_1, Y_2, . Y_, X_1, X_2, . X_k$.

Бележка 2. По-горе разгледахме графиката $\Gamma (V,R)$ като линейно картографиране от пространството $W_$ към пространството $W_$, картографирайки всеки ръб на графиката към неговите крайни върхове и показахме, че това линейно картографиране съответства на матрицата на инцидентност $B$ на тази графика. Заедно с това картографиране можем да разгледаме линейно картографиране от пространството $W_$ към пространството $W_$, което картографира всеки връх към набора от ребра, инцидентни на този връх. Лесно се вижда, че матрицата на това линейно преобразуване в "каноничните бази" на пространствата е матрицата $B^T$. Също така е лесно да се види, че елементите на ядрото на това картографиране ще съответстват на свързаните компоненти на графиката и обединенията (в този случай „директни суми“) на компонентите. Дадохме този пример, без да даваме подробно изследване на картографирането, тъй като е типично за изграждане на множество аналози.Нека обърнем внимание на факта, че в нашия пример елемент от множеството $V$, някакъв връх, се преобразува в подмножества от два елемента на множеството $V$, т.е. на ребра, които от своя страна са елементи от множеството $R$. Пример за преобразуване на елементи в подмножества, към които принадлежи този елемент, е типичен и съответните матрици на тези преобразувания се наричат (като правило, не в теорията на графите) матрици на инцидентност. Така в теорията на графите се появява "матрица на разфасовките", съответстваща на преобразуването на множеството $R$ в множеството разрези (всяко ребро се преобразува във всички разрези, в които влиза), "матрицата на циклите" - съответстващо на преобразуването, което свързва с всяко ребро цялото множество от цикли, в които това ребро влиза (вижте например монографията, цитирана в параграф 15). Матриците от разрези и цикли са намерили приложение както в теорията на графите, така и в нейните приложения.

Обърнете внимание, че щом ни бъдат дадени две векторни пространства, дефинирани върху едно и също поле, например над полето $GF(2)$, тогава имаме възможност да разгледаме линейни преобразувания на едно пространство в друго. Най-лесният начин да направите това е в координатните пространства, съответстващи на дадените пространства, тъй като в този случай линейните преобразувания могат да бъдат зададени чрез матрици.