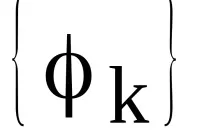
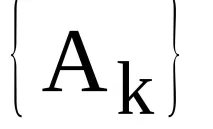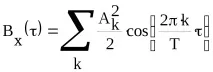3 Корелационен анализ на сигнали
Смисълът на спектралния анализ на сигналите е да се проучи как сигналът може да бъде представен като сума (или интеграл) от прости хармонични трептения и как формата на сигнала определя структурата на честотното разпределение на амплитудите и фазите на тези трептения. За разлика от това, задачата на корелационния анализ на сигналите е да се определи мярката за степента на сходство и разлика между сигнали или изместени във времето копия на един сигнал. Въвеждането на мярка отваря пътя към количествени измервания на степента на сходство на сигнала. Ще бъде показано, че съществува определена връзка между спектралните и корелационните характеристики на сигналите.
3.1 Автокорелационна функция (acf)
Автокорелационната функция на сигнал с крайна енергия е стойността на интеграла от произведението на две копия на този сигнал, изместени едно спрямо друго с време τ, разглеждано като функция на това времево изместване τ:
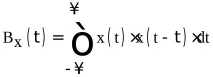
Ако сигналът е дефиниран на краен интервал от време

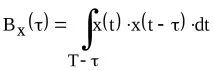
където
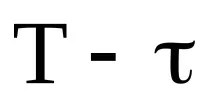
Смята се, че колкото по-голяма е стойността на автокорелационната функция
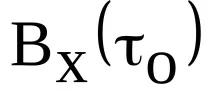
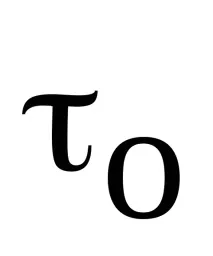
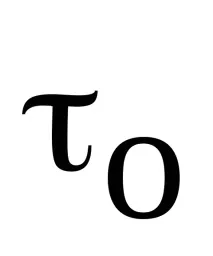
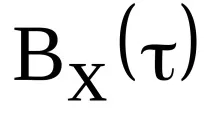
Мярката за подобие, въведена по този начин за сигнали, които имат формата на случайни флуктуации около нулата, има следните характерни свойства.
Ако изместените копия на сигнала осцилират приблизително във времето един с друг, това е знак за тяхното сходство и ACF приема големи положителни стойности (голяма положителна корелация). Ако копията осцилират почти извън фаза,ACF приема големи отрицателни стойности (анти-подобие на сигнални копия, голяма отрицателна корелация).
Максималната ACF се постига, когато копията съвпадат, тоест при липса на смяна. Нулеви стойности на ACF се постигат при смени, при които не се забелязва нито сходство, нито антисходство на копията на сигнала (нулева корелация, липса на корелация).
Фигура 3.1 показва фрагмент от изпълнението на някакъв сигнал във времевия интервал от 0 до 1 s. Сигналът произволно осцилира около нулата. Тъй като интервалът на съществуване на сигнала е краен, тогава неговата енергия също е крайна. Неговата ACF може да се изчисли съгласно уравнението:
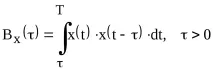
Автокорелационната функция на сигнала, изчислена в MathCad в съответствие с това уравнение, е показана на фиг. 3.2. Корелационната функция показва не само, че сигналът е подобен на себе си (отместване τ=0), но също така, че копията на сигнала, изместени едно спрямо друго с приблизително 0,063 s, имат известно сходство (латерален максимум на автокорелационната функция). За разлика от това, копията на сигнала, изместени с 0,032 s, трябва да бъдат анти-подобни дъги една спрямо друга, тоест да бъдат в известен смисъл противоположни една на друга.
Фигура 33 показва двойки от тези две копия. От фигурата може да се проследи какво се има предвид под сходство и антиподобие на сигнални копия.
Корелационната функция има следните свойства:
1. При τ = 0 автокорелационната функция приема най-голямата стойност, равна на енергията на сигнала
2. Автокорелационната функция е четна функция на времевото изместване.
3. С увеличаване на τ автокорелационната функция намалява до нула
4. Ако сигналът не съдържа прекъсвания като δ - функции, тогава
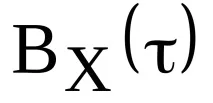
5

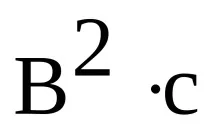
За периодични сигнали в дефиницията на автокорелационната функция същият интеграл се разделя на периода на повторение на сигнала:
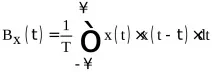
Така въведената корелационна функция има следните свойства:
стойността на корелационната функция при нула е равна на мощността на сигнала
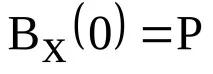
размерността на корелационната функция е равна на квадрата на размерността на сигнала, например

Например, нека изчислим корелационната функция на хармонично трептене:
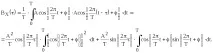
Използвайки серия от тригонометрични трансформации, накрая получаваме:
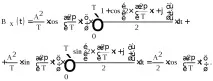
По този начин автокорелационната функция на хармонично трептене е косинусова вълна със същия период на промяна като самия сигнал. При смени, които са кратни на периода на трептене, хармоникът се преобразува в себе си и ACF приема най-големите стойности, равни на половината от квадрата на амплитудата. Времевите измествания, които са кратни на половината от периода на трептенето, са еквивалентни на фазово изместване под ъгъл
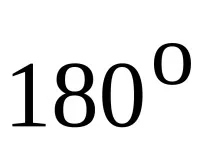
Важно е изразът за корелационната функция на сигнала да не включва началната му фаза. Информацията за фазата се губи. Това означава, че самият сигнал не може да бъде реконструиран от корелационната функция на сигнала. Преобразуването
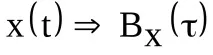
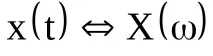
Ако под механизмаза да разберем определен демиург, който създава сигнал според избраната от него корелационна функция, тогава той би могъл да създаде цял набор от сигнали (ансамбъл от сигнали), които наистина имат една и съща корелационна функция, но се различават един от друг във фазовите отношения.
Актът за избор на началната фаза може да се разглежда като:
акт на проявление по сигнал на свободна воля, независим от волята на твореца (възникването на отделни реализации на някакъв случаен процес),
резултатът от външно насилие върху сигнала (въвеждане в сигнала на измервателна информация, получена по време на измерване на някакво физическо количество).
Същото важи и за всеки периодичен сигнал. Ако периодичен сигнал с основен период T има амплитуден спектър