3. РАЗДЕЛЕНИЕ НА ОКРУГ НА РАВНИ ЧАСТИ И ПОСТРОЯВАНЕ НА ПРАВИЛНИ МНОГОГОЛНИЦИ
3.1. Определяне на центъра на дъга
Вземете на дъга от окръжност (фиг. 21) три произволно разположени точки A, B и C. Отсечките AB и BC са хордите на дадената дъга. Пресечната точка на перпендикулярите, прекарани през средните точки на хордите, определя позицията на центъра O на първоначалната дъга. Конструкцията се основава на дефиницията на окръжност като геометрично множество от точки, отдалечени от центъра на дадено разстояние R.

3.2. Определяне на центъра на окръжност
В даден кръг (фиг. 22) начертайте две неуспоредни една на друга хорди AB и CD. Начертайте перпендикуляри през средните точки на хордите, чието пресичане определя позицията на центъра O на оригиналния кръг.
3.3. Разделяне на кръг на три, шест и дванадесет части
В окръжност с даден радиус R (фиг. 23) начертайте взаимно перпендикулярни диаметри AB и CD през центъра O. От всяка точка на края на диаметъра (например от точка А) начертайте дъга с радиус R \u003d AO, докато се пресече с кръг в точки 1 и 2. Отсечка 12 е търсената страна на правилен вписан триъгълник 1 В 2 .
Сегменти A 1 \u003d A 2 и C 1 \u003d D 2, съответно, са равни на страните на правилните вписани шестоъгълници и додекагони. За да построите липсващите върхове на многоъгълниците, достатъчно е да начертаете дъга със същия радиус R от противоположния край на диаметъра на кръга (в нашия случай от точка B) до пресечната точка с кръга.
3.4. Разделяне на кръг на четири и осем части
Начертайте два взаимно перпендикулярни диаметъра AB и CD (фиг. 24). Отсечките AC = CB = BD = DA, свързващи краищата на диаметрите, са страни на правилен вписан четириъгълник.
За да разделите кръга на осем части, е необходимо да построите перпендикуляри към средните точки на страните на четириъгълника и да ги продължите, докато се пресекат скръг. Отсечката AM е страната на правилен осмоъгълник, вписан в окръжност.
3.5. Разделяне на кръг на пет и десет части
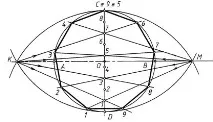
Начертайте два взаимно перпендикулярни диаметъра AB и CD (фиг. 25) и разделете радиуса OB наполовина в точката M. От точка M, както от центъра, начертайте дъга с радиус MC, докато се пресече с диаметър AB в точка K. Отсечката CK е равна на страната на правилен вписан петоъгълник, отсечката OK е равна на страната на правилен вписан десетоъгълник.
3.6. Разделяне на кръг на седем части
От точки A и B на краищата на хоризонталния диаметър AB (фиг. 26) начертайте дъги с радиус R = AO = BO и маркирайте точките на тяхното пресичане 1 и 2 с оригиналната окръжност.
В пресечната точка на хорда 12 с радиус OD, маркирайте точка М. Отсечката OM е равна на страната на правилен вписан седмоъгълник. За да го конструира, измервателният уред последователно поставя съответните сегменти върху оригиналния кръг.
3.7. Разделяне на кръг на n равни части
Начертайте два взаимно перпендикулярни диаметъра AB и CD в окръжност с даден радиус R (фиг. 27) и разделете един от диаметрите, например CD, на даден брой равни части (n = 9). От точки C и D, както от центрове, начертайте дъги от окръжности с радиус 2 R, докато се пресекат с диаметър AB в точки K и M.
Използвайки получените точки K и M като центрове, начертайте семейство лъчи през четни или нечетни (както в нашия случай) разделителни точки на диаметъра CD, докато се пресекат с дадена окръжност. Точки 1 , 2 , получени върху окръжността. . . , 9 са желаните точки за разделяне на кръга на даден брой части. Описаният метод е приблизителен; дъгите, на които е разделена окръжността, всъщност не са равни една на друга. Грешката обаче не надвишава 0,01 R, което за практически цели може да бъдесмятат за достатъчно.
3.8. Построяване на правилни многоъгълници по дадена страна
Разделете страната AB (фиг. 28) от точка O наполовина и възстановете в тази точка перпендикуляра на сегмента AB. Начертайте дъги с радиус R = AB от точки A и B, докато се пресекат в точка 1. Триъгълник A 1 B е търсеният равностранен триъгълник.
За да се построи квадрат, е необходимо да се възстановят перпендикулярите на сегмента AB в точки A и B и да се продължат, докато се пресекат в точки C и D с дъги с радиус R = AB. Квадратът ACDB е желаният.
Начертайте диагонали в квадрата ACDB и отбележете точка 2 на тяхното пресичане. Разделете разстоянието между точки 1 и 2 наполовина с точка 3, която ще служи като център на окръжността за вписан в нея правилен петоъгълник със страна AB.
Последователно отлагайки разстоянието 13 от точка 1 нагоре по перпендикуляра, маркирайте точки 4, 5, 6,. . . , n , които ще служат като центрове на окръжности за