§ 3. Сравнение на две регресии

Това обикновено е типично за времеви редове от икономически данни, когато се променят институционалните условия, въвеждат се нови законови или данъчни ограничения. Например, може да се предположи, че до определена година в страната обменният курс е бил фиксиран, а след това плаващ, или данъкът върху вносните автомобили е бил един, а след това се е променил значително. В този случай зависимостта може да се изрази по следния начин:

Фиктивната променлива D в уравнение (7.5) се използва както в адитивна форма (y1D), така и в мултипликативна форма (y2DX), което всъщност ни позволява да разделим разглежданата зависимост на две части, свързани с периодите на промяна на някакъв качествен фактор, разглеждан в модела. Регресионно уравнение

доста добре моделира ситуацията, изобразена на фиг. 7.1-7.2.

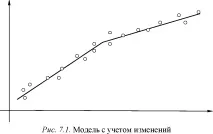
На фиг. 7.1, моделът отчита промените, настъпили от определен момент в естеството на местоположението на точките за наблюдение. Има ли смисъл да изградим сложна регресия с фиктивни променливи (фиг. 7.1) или да се ограничим до „обикновена регресия“ (фиг. 7.2)? На този въпрос може да се отговори с помощта на теста Chow. Нека извадката е n. Означаваме с S0 сумата от квадратите на отклоненията на стойностите y от общото регресионно уравнение (фиг. 7.2).

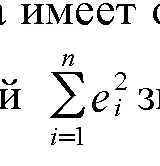
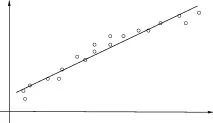
Ориз. 7.2. Модел без отчитане на промени Нека има причина да се приеме, че е препоръчително общата проба да се раздели на две подпроби с обеми n1 и n2, съответно jn = n1 + n 2) и да се състави регресионно уравнение за всяка от пробите (фиг. 7.1). Означаваме с lt;S1 и S2 сумите на квадратите на отклоненията на стойностите на y, всяка от подизвадките от съответните регресионни уравнения. Очевидно равенството S0 = S1 + S2 е възможно само ако регресионните коефициенти за трите уравнения (7.5-7.7) съвпадат. Разлика S0— (S1 + S2) може да се тълкува като подобрение в качеството на модела, когато интервалът на наблюдение е разделен на два подинтервала. Дробта [S0 - (S1 + S 2)1 jm + 1) определя оценката на намалението на дисперсията на регресията поради конструирането на две уравнения вместо едно. В този случай броят на степените на свобода ще бъде намален с jm +1) , тъй като вместо jm +1) на параметъра на комбинираното уравнение, сега е необходимо да се оцени j2m + 2) на параметъра на две регресии.

Ако намалението на дисперсията не е статистически различно от необяснената дисперсия, тогава конструираната А-статистика има разпределение на Фишер със степени на свобода v1 = m + 1 и v2 = n - 2m - 2. Тук m е броят на количествените обяснителни променливи в регресионните уравнения (m е еднакъв и за трите регресионни уравнения). Тогава, ако Anabl, изчислена по формулата (7.8), е по-малка от съответната критична точка на разпределението на Фишер при избраното ниво на значимост a

тогава се счита, че разликата между S0 и S1 + S 2 е статистически незначима и няма смисъл регресионното уравнение да се разделя на части. В противен случай разделянето на подинтервали е препоръчително от гледна точка на подобряване на качеството на модела. Това всъщност означава необходимостта от въвеждане на съответната фиктивна променлива в регресионното уравнение. Тестът Chow е напълно достатъчен, ако искате да установите, че зависимостите в подпробите са различни. Резюме Фиктивните (двоични) променливи приемат стойности от 0 или 1. Тяхната "фиктивност" се състои единствено във факта, че те описват количествено качествен атрибут. Броят на двоичните променливи е с една единица по-малък от броя на алтернативите на качествен признак (правилото трябва да се прилага за всеки признак поотделно). Ако качествена характеристика е включена в модела допълнително, тогава това води до паралелно изместване на графикатапо оста на зависимата променлива. Ако една качествена характеристика влезе в модела мултипликативно, това води до промяна в наклона на правата линия. Въпроси за самопроверка

Какви стойности могат да приемат обяснителните фиктивни променливи?
Една качествена характеристика има три алтернативи, колко фиктивни променливи трябва да се използват в модела, за да се опише?
Има две качествени характеристики, всяка с три алтернативи, колко фиктивни променливи трябва да се използват в модела?
Какво се случва с графиката на сдвоеното уравнение на линейна регресия, ако в модела се въведе една допълнителна двоична променлива?
Какво ще се случи с графиката на сдвоената линейна регресия, ако една двоична променлива се въведе в модела адитивно и мултипликативно?
Каква е разликата между моделите ANOVA и ANCOVA?