3.1.4 Асоциирани и обратни матрици

IfA-is a square matrix, aCij-is an algebraic complementaij,thenadjointforAis a matrix formed from algebraic complementsCji,i.e.

Така присъединената матрица (Adj– според първите букви на английската дума adjust – адаптирам, напасвам, прикрепям) се транспонира за матрицата, образувана чрез замяна на елементиаijс техните алгебрични допълнения.

Уравнение (3.4) предполага това

Като вземем предвид дефиницията (3.6) и умножим дясната и лявата част на последния израз по1/A (при условиеA0), получаваме

(3,7)

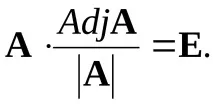
От израз (3.7), обратната матрицаA-1

(3,8)

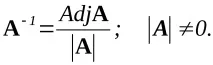
Лесно е да се покаже, че връзката

Наистина, нека вземем тъждествотоA-1=A-1и умножавайки дясната и лявата му страна поEотдясно, докатоEот лявата страна на тъждеството записваме съгласно връзката (3.9):

Използвайки свойството на единичната матрица и асоциативността на умножението, получаваме

откъдето неизбежно следва (3.10).

Следователно матрицата и нейната обратна са комутативни. Ако A=0, тогава матрицатаAсе наричаспециална. АкоA0, тогава матрицата се наричанеособена. Следователно обратни матрици съществуват само за неособени матрици.

От израз (3.8) следва, че обратната матрица за всяка неособена матрица е уникална и следователно наборът от неособени квадратни матрици образува некомутативна група чрез умножение.

Произведението на обратните матрици се подчинява на същите правила за пермутация като произведениетотранспонирани матрици, т.е

Производната на обратната матрица се изчислява по формулата

(3.11)

което е лесно да се получи, ако разгледаме връзката

Някои специални обратни матрици имат отделни имена.

Инволютивнатаматрица е матрица, която съвпада със своята обратна, т.е.AA=E.

Ортогоналнатаматрица е матрица, за която е изпълнено отношениетоA-1 =AT.

Унитарнатаматрица удовлетворява отношениетоA=((A*) T ) -1 .

Псевдо-обратнатаматрица

удовлетворява отношенията

(3.12)

(3,13)

(3,14)

(3,15)

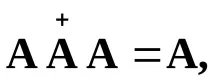
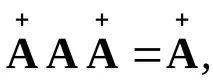
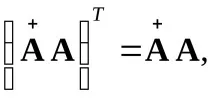
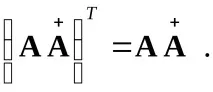
Ако отношенията (3.14), (3.15) (едно от тях или и двете) не са изпълнени, тогава получавамеобобщена обратнаматрица.

Разбира се, в случай на неизродена матрицаA, псевдообратната и обобщената матрици съвпадат с обичайната обратна матрица.

3.2 Вектори и векторни пространства

3.2.1 Вектори и техните свойства

Под вектор ще разбираме матрица с размерност(n1)или вектор-колона.

Нека дефинираме основните операции върху вектори.

Скаларното произведение (или вътрешно произведение) на два вектораxиyсе определя от формулата

В случай на реалниxиyизразът (3.16) приема по-позната форма

=

=xTy=yTx= .

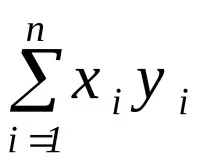
Ясно е, че концепцията за скаларно произведение съществува само за вектори с една и съща размерност.

.

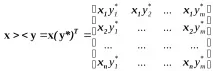
Сумата и разликата на векторите, както и умножението на вектор по скалар, следват от съответните операции върху матрици.

Двата вектора се наричатортогонални, ако тяхното скаларно произведение е равно на нула.

Норматана вектор е корен квадратен от скаларното произведениеxиy, т.е.

(3,17)

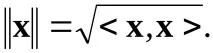
Може да се покаже, че връзката (3.17) предполага две важни неравенства

(неравенство на триъгълник)

и (неравенство на Шварц).

Ъгълътмежду два вектора се определя по формулата

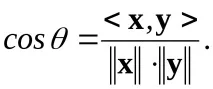
Вектор

се наричанормализиранако.

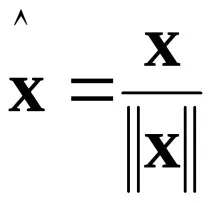
Два вектора ще бъдатортонормални, ако са ортогонални и нормализирани.

Въз основа на концепцията за линейна независимост на векторите, даваме още няколко дефиниции.

Дегенерацияилидефектна матрица се дефинира както следва. Ако редовете (колоните) на сингулярна матрица са линейно свързанис еднарелация, тогава израждането на матрицатае просто(дефектът е равен на единица). Ако такива отношенияq, тогава матрицата има дегенерация на множественостq(или дефектът е равен наq).

Рангrна матрицаAе най-високият порядък на ненулевите минори на матрицаA. Ако размерността на матрицата(nn),тогаваr=n-q.

Съществува правило за израждане на Силвестър, което гласи, че дефектът на произведението на две матрици не е по-малък от дефекта на всяка от тях и не е по-голям от сумата от дефектите на матриците.

Условието за линейна независимост на векторите може да бъде формулирано въз основа на ранга на матрицата, образувана от елементите наmвектори:

(3,19)

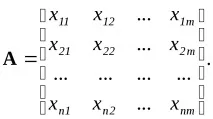
Тази система от хомогенни уравнения има нетривиално решение заki(т.е. условие (3.18) е изпълнено и векторитеxiса линейно зависими) само ако детерминантата на матрицата с елементи е равна на нула. Тази детерминанта се нарича детерминанта на Грам и е равна на

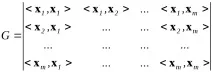
или, като се вземе предвид нотацията (3.19),

Следователно, система от вектори е линейно независима тогава и само ако детерминантата на Грам (3.20) за такава система е различна от нула.

---