4 души си подадоха ръка
За да разрешите такива проблеми, най-удобно е да начертаете диаграма. Множество точки. Броят на точките съответства на броя на хората. След това свържете всички точки заедно. Тук броят на сегментите ще бъде равен на броя на ръкостисканията.
В този случай получаваме 6 ръкостискания.
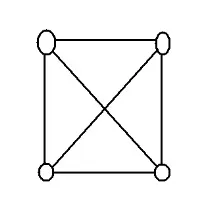
Тъй като задачата е от учебника Логика (Холодов) за 4 клас, ще решим задачата по схемата. Начертайте 4 точки и свържете всяка с всяка със стрелки. Получават се 6 стрели, тоест 6 ръкостискания.

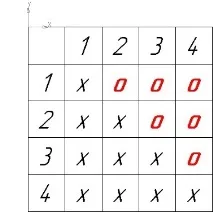
Най-лесният начин да се справите със задачата ще бъде таблицата по-долу, където червените нули са ръкостискания, а кръстовете са същите ръкостискания, но които не трябва да се броят, тъй като вече са дублирани. Нека преброим и да получим верния отговор в размер на шест перфектни ръкостискания.
По прост начин. Първият се ръкува с другите трима. Общо три. Вторият вече се справи с първия, останаха два и ги добавяме. Първият и вторият вече са си подали ръцете с третия, остава четвъртият, добавяме го сам. Получаваме общо шест.
Научен. Имаме n=4 елемента, които образуват комплекти от k=два. В комбинаториката броят на комбинациите от n до k е n! /k!*(n-k)! Факториелът на четири е 24, факториелът на две е 2 и факториелът на 4-2 също е две. Разглеждаме: 24 / (2*2) = 24/6 = 6
Много научен. Теория на графите. Пълен граф е този, в който всяка двойка отделни върхове е съседна. В контекст – всеки се ръкува с всеки. Имаме n=4 върха, броят на ръбовете на пълния граф е n(n-1) / 2 = 4*3 / 2 = 6
Вече имаше подобен въпрос в BV. Или може би точно същото.
Първият поздрави останалите трима.
Вторият човек, останал да поздрави двама,в крайна сметка той вече поздрави първия.
Третият вече поздрави първите двама, остава да поздрави само последния от четиримата.
3 плюс 2 плюс 1 общо 6 ръкостискания.
Всеки човек от тази четворка може да се ръкува с други трима.
Общо 4 по 3, получавате 12 ръкостискания. Но тъй като в ръкостискането участват двама души, разделянето му ще отнеме 12 към 2. Общо се получават 6 ръкостискания.
Този проблем може да бъде решен по няколко начина: и с помощта на таблици, сортиране през всички възможни опции и по този начин идентифициране на отговора на поставения въпрос, както и решаване с помощта на добре познати комбинаторни формули.Само в този случай е необходимо правилно да зададете първоначалния проблем.Така че според първия метод ще разгледаме метода за изброяване на различни опции за ръкостискане между четирима души.
1) Номер 1 ще се ръкува 3 пъти с другите.
2) Номер 2 също ще доведе до 3 ръкостискания, но 1 ръкостискане вече е взето предвид в предишното изчисление и получаваме: 3-1=2 ръкостискания.
3) Номер 3 относно обяснението на аналогията: 3-1-1=1 ръкостискане.
4) Номер 4 вече е взет предвид във всички опции за ръкостискане: 3-1-1-1=0.
ОБЩО: (3+2+1)=6 ръкостискания И това е отговорът.
2 опция за изчисление) - според формулата на комбинаториката: използвайки формулата за комбинация: броят на комбинациите от 4 до 2 \u003d От 4 до 2 \u003d (4!) \ (2! * 2!) \u003d (1 * 2 * 3 * 4) \ (2 * 1) * (2 * 1) = 2 * 3 \u003d 6 (ръкостискания).