47 Ойлерови вериги и цикли
цикълът, съдържащ всички ребра на графиката, се наричаОйлерова линия,Ойлеров цикъл, затворена Ойлерова верига или просто
Ойлерова верига. Графиката, съдържаща цикъла на Ойлер, се наричаграфика на Ойлер. Ако графиката съдържа отворена верига, съдържаща всички ребра на тази графа, тогава такава графа се наричаполу-ойлерова.
Теорема 1.Ако всички върхове в свързана графа са четни, тогава тази графика съдържа цикъл на Ойлер.
Обратното също е вярно: ако графът съдържа цикъл на Ойлер, тогава всичките му върхове са четни.
Теорема 2.Ако два върха в свързан граф са нечетни и всички останали върхове са четни, тогава този график съдържа отворена верига на Ойлер.
Всяка линия, която може да бъде начертана, минаваща през дадените секции точно веднъж, се наричаеднокурсова
Теорема 3.Ако свързан граф G съдържа 2k нечетни върха, тогава той има k отворени вериги на Ойлер, съдържащи всички ребра на графа G точно веднъж.
Теорема 4.Във всяка свързана графа е възможно да се конструира затворен маршрут, минаващ през всяко ребро точно два пъти.
От теорема 4. следва, че всяка графика може да бъде начертана, без да се вдига моливът от хартията и да се минава през всеки ръб не повече от два пъти.
цикъл, съдържащ веднъж всеки връх на графиката, се наричахамилтоновалиния (хамилтонов цикъл), а графика, съдържаща хамилтонова линия, се наричахамилтонова.
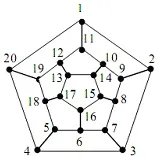
Свързан граф, съдържащ проста отворена верига, която включва всички върхове на графа, се наричаполухамилтонов.
Верига(цикъл) в G се наричахамилтониан(хамилтониан), ако тя (той) преминава веднъжпрез всеки връх на псевдографа G.
Графикаехамилтонова, ако съдържа хамилтонов цикъл.
Теорема.Ако в проста графа с n (і 3) върха локалната степен на всеки връх е най-малко , тогава графиката е Хамилтонова.
48 Транспортни мрежи. Концепцията за транспортна мрежа.
Транспортната мрежа е диграф D = (V, X) с набор от върхове V, за които са изпълнени следните условия:
1) има един и само един връх V1, наречен източник, такъв, че D на степен (-1) (V1) = 0 (тоест няма дъга да влиза във V1);
2) има един и само един връх vn, наречен потъване, така че D(vn) = 0 (т.е. от vn не излизат дъги);
3) на всяка дъга x О X се приписва цяло число c(x)0, наречено капацитет на дъгата.
Определение. Върховете в транспортната мрежа, различни от източника и приемника, се наричат междинни.
Функцията j (x), дефинирана върху множеството X от дъги на транспортната мрежа D и приемаща цели числа, се нарича допустим поток (или просто поток) в транспортната мрежа D, ако:
1) за всяка дъга x О X стойността j(x), наречена поток по дъгата x, удовлетворява условието 0j(x)c(x);
2) за всеки междинен връх v е в сила следното равенство:
тези. сумата от потоци по дъги, влизащи в v, е равна на сумата от потоци по дъги, излизащи от v.
49 Поток в транспортната мрежа. Разрез, производителност на разреза.
Определение. Стойността на потока j в транспортната мрежа D е стойността j, равна на сумата от потоците по всички дъги, влизащи в , или, което е същото, стойността, равна на сумата от потоците по всички дъги, излизащи от V1, т.е.:
Определение. Една дъга x ⊂ X се нарича наситена, ако потокът по нея е равен на нейнияпропускателна способност, т.е. ако j(x)= c(x) Поток j се нарича завършен, ако всеки път в D от V1 до Vn съдържа поне една наситена дъга.
Определение. Потокът j се нарича максимален, ако стойността му придобива максимална стойност в сравнение с други допустими потоци в транспортната мрежа D.
Очевидно е, че максималният поток j е задължително пълен. Обратното не е вярно. Има пълни потоци, които не са максимални. Въпреки това общият поток може да се разглежда като някакво приближение до максималния поток.
Разделителното множествона граф G е такова множество от неговите ребра, след премахването на които се получава несвързан граф.Изрязванее разделящо множество, което няма разделящо собствено подмножество.
Разрезът на мрежата е наборът, който притежава източника и не принадлежи към изтичането. Тези. разрезът е минимален (в смисъла на връзката на включване) набор от дъги, премахването на които „разрушава“ всички пътища, свързващи източника и поглъщането.
Пропускателната способност на разрез е число, равно на сумата от пропускателните способности на дъгите на този разрез. Разрезът се нарича минимален, ако има най-малката производителност.
Намирането на минималния разрез е една от основните задачи при анализа на транспортните мрежи.
Тъй като графиката е крайна, минималното разрязване може да бъде намерено чрез изброяване на всички разрези, но този път, разбира се, е неприемлив за достатъчно големи графи. Оказва се, че минималното разрязване може да се намери с помощта на максималния поток на мрежата въз основа на теоремата на Форд-Фулкерсън.