№ 49*. Докажете, че ако лъч, излизащ от върха на ъгъл, пресича сегмент AB с краища от страните на ъгъла, тогава той пресича 1) сегмент AC с краища от страните на ъгъла; 2) всеки сегмент CD с краища отстрани на ъгъла.

1) Нека K е пресечната точка на лъча с отсечката AB. Правата OK пресича отсечката AB, следователно точките A и B лежат в различни полуравнини спрямо правата OK. Точките B и C лежат в една и съща полуравнина, тъй като отсечката BC не се пресича с правата OK, а точките A и C лежат в различни полуравнини, откриваме, че правата OK пресича отсечката AC в някаква точка, означена с буквата E.
Правата BC разделя равнината на две полуравнини, едната от които съдържа дадения лъч OK и точката A (тъй като отсечката AK не пресича правата OB) и точката E (тъй като отсечката AE не пресича правата OB). Следователно точката E трябва да лежи на лъча OK.
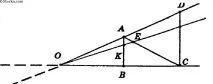
2) Нека CD е произволен сегмент с краища от страните на ъгъла и точката C лежи на страната OB, а точката D лежи на страната OA. Отсечката AB пресича лъча OK, което означава, че лъчът OK пресича и отсечката AC, а ако лъчът пресича AC, то лъчът ще пресича и отсечката CD.