5 Анихилиращи полиноми
10 Теорема на Хамилтън–Коши
P(x) полином върху k
Тогава полином в оператор е такъв анихилиран полином, който се получава чрез заместване на оператора за h
Определение: A:LL P(x) - полиномът се нарича анихилиращ полином на оператора A или анихилатор, ако равенството
Анихилиращ полином се нарича минимален, ако, първо, той е анихилатор и, второ, има най-малка степен сред другите анихилатори.
P(A)(e 2x )=(A-2E) 2 (A-2E)(e 2x )= (A-2E) 2 (2e 2x -2e 2x )=0
P(A)(x 2 e 2x )=(A-2E) 2 (A-2E)(x 2 e 2x )=(A-2E) 2 (2xe 2x +2x 2 e 2x -2x 2 e 2x )=(A-2E)(A-2E)(2xe 2x )=(A-2E)(2e 2x +4xe 2x - 4xe 2x)=0
P(A)=(A-2E) 3 отменя всички вектори и следователно цялото производство
Лема: Ако A:LL, тогава съществуващата нула (dimL 2
doc, разгледайте основата e1,…,en – разгледайте Ae e
(Ae e ) 0 , Ae e ,( Ae e ) 2 ,…( Ae e ) n^2 n^2+1 матрица - LZ
0(
P(x)*Q(x) – същия анихилатор
Лема 3: най-високото anul pl може да бъде разделено на минималното anul pl.
Deg(r) 2 e 2x, xe 2x, e 2x >
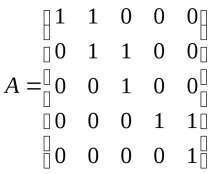
Jn(l)=
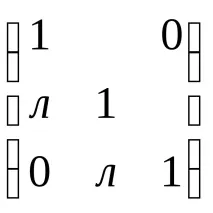
Jk 2 (O)=
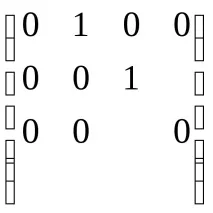
Първата матрица се нулира на 3-та стъпка
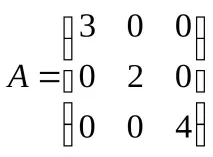
мощности на един оператор за пермутация.
Лема: 4 Ако в линейно пространство LM е инвариантно, тогава XA(A)=XA(A/M)Q(x)
e1…ek е основата на M, допълнение към основата
Теорема на Хамилтън Кейли.
Теорема: (Хамилтън Кейли) A:L L
Характеристичният полином е анихилаторът на цялото пространство Xa(A)=0
Доказателство: (Само за алгебрично затворено поле) доказателството е чрез индукция върху размерността на пространството.
а) Нека dim L=1, тогава A:LL е умножение по число.
A(x)=x ако x0,след това формира основа.
b) Да приемем XA(A)>0, ако dim L N+1, тъй като полето е алгебрично затворено
разгледайте Xa(), съществува е собствена стойност и има собствен вектор e1
Нека вземем този вектор и го допълним до основата e1, e2…eN+1
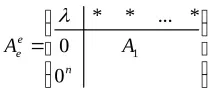
Да разгледаме линейната обвивка на собствения вектор M=Z1> и факторно пространство L/M=
В частното пространство операторът A=A генерира A:L/ML/M
Ax=Ax=Ax+M
Вектори в частното пространство e2+M1e3+…+M1eN+1– базисно L/M частно пространство => тогава А1– е матрица А1– матрицаА в този базис
dimL/M=N=> XA(t) е анихилаторътИ това означава, че ако заместим X вместо t
XA1(A)= XA(A) е нулевият оператор в пространството L/M
Това означава, че XA1(A)x= XA1(A)x+M)= XA1(A)x+M е нулевият клас
Следствие: Всеки min анихилатор е делител на характеристичния полином на оператора.
6. Йорданова канонична форма на линеен оператор.
Дефиниция: Jk()=
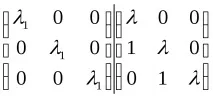
Матрицата се нарича клетка на Йордания, ако е Cell Diagonal с квадратни блокове и всеки от тях е клетка на Jordan.
J=
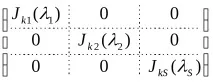
Теорема: Нека А:LL се нарича алгебрично затворено поле, тогава съществува базис, в който матрицата на този оператор е йорданова.
Матрицата на Джордан е уникална до пермутация на клетката, основата на Йордан е дефинирана по неуникален начин.
Теорема: k е алгебрично затворено поле L е линейно пространство над k
Ae e=
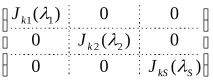
Има основа е1…е2: Аe e =
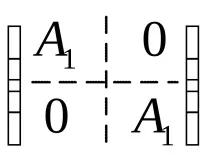
Ако L се разложи на пряка сума на инвариантно пространство, тогава е достатъчноконструирайте Йорданова форма на ограничение до няколко подпространства и след това комбинирайте.
Определение A:LL, коренното подпространство L(, съответстващо на числото, е множеството xL, което удовлетворява условието (A-E) r x=0
Забележка: всеки собствен вектор за даден е корен със стойност r=1
Най-малкото от всички r за даден коренен вектор се нарича неговата височина.
L() тогава и само ако е собствена стойност.
L() е линейно пространство.
Нека XA) е характеристичният полином на A, полето е алгебрично затворено, => всеки полином има корен.
Нека разложим XA на множители.
Li() – образува оператор.
Нека докажем, че пространствата в 2 и 3 съвпадат.
И че цялото пространство е сумата от Li()
Нека заместим оператора вместо единица
прилагаме оператора за идентичност
тези. векторът е написан като сума от вектори, лежащи в пространства, всеки вектор може да бъде представен като сума от членове, всеки от които лежи в пространство.
Нека докажем, че сумата е пряка.
L=L1(1)L2(2)LS(S), да предположим, че векторът X лежи в пресечната точка на едно от тези пространства със сумата.
XA - анулира цялото пространство чрез теоремата на Хамилтън Кейли, т.е. това изображение 0
необходимо е да се докаже, че ако векторът е корен, тогава той лежи в Li(i)