5.7 Сравняване на множество проби
За да сравните множество проби, използвайте:
дисперсионен анализ за случай на нормално разпределени променливи с равномерни дисперсии;
непараметрични тестове - за разпределения, различни от нормалното и за малки извадки.
За сравняване на повече от две независими проби по отношение на нивото на изразяване на променливите се използват няколко критерия: H-тест на Kruskal (Kruskal (-Wallace (Wallis), тест за медиана, тест на Jonkier-Terspt. От тях тестът на Kruskal-Wallis има най-висока чувствителност към разликите. Този тест е непараметричен аналог на дисперсионния анализ. Разликите са, че:
не се сравняват средните стойности на променливите, а средните стойности на техните рангове;
Не се използва F-тестът на Фишер, а тестът хи-квадрат.
Дисперсионният анализ дава по-точни резултати, но условието за използването му е нормалното разпределение на стойностите на признаците и хомогенността на дисперсиите или достатъчно голям размер на извадката.
За малки проби и разпределения, които се различават от нормалните, се препоръчва използването на теста на Kruskal-Wallis.
5.7.1 Сравнение на няколко независими проби. Тест на Крускал-Уолис
Тестът на Kruskal-Wallis е предназначен да тества равенството на медианите на няколко проби. Това е обобщение на U-теста на Mann-Whitney за случай на
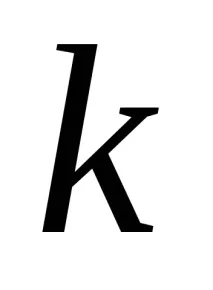
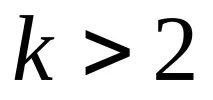
Критерият на Kruskal-Wallis е рангов, така че е инвариантен по отношение на всяка монотонна трансформация на измервателната скала.
Стойностите на атрибутите са класирани за всички проби, като за една, във възходящ ред. След това изчислете сумата от ранговете за всекипроби отделно. Пробите могат да бъдат с различни или еднакви размери.
Емпиричната стойност на теста на Kruskal-Wallis се изчислява по следната формула:
,
където

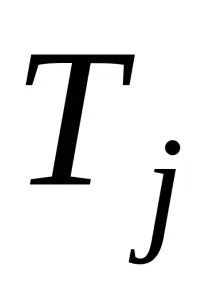

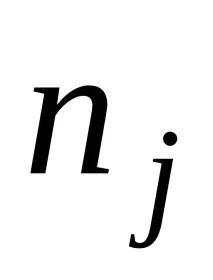

Нулевата хипотеза за изместване се отхвърля при ниво на значимост

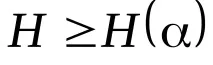
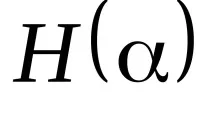
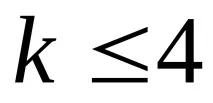
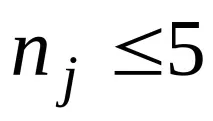
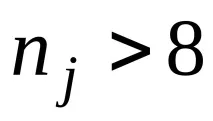
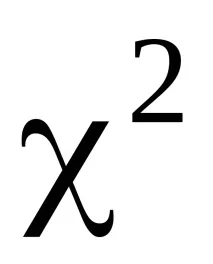
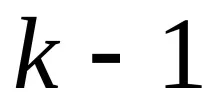
Схемата за прилагане на критерия Крускал-Уолис е следната
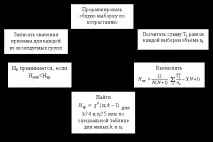
Фигура 1 Алгоритъм за прилагане на критерия на Крускал-Уолис
Пример за използване на теста на Kruskal-Wallis
Еднаква ли е степента на усвояване на нов материал от младши и старши ученици и учители?