6. Тестване на надеждността
6.1. Значение и видове тестове за надеждност
Тестът за надеждност е задължителен вид тестване. Тяхната обща цел е да установят надеждността на продуктите при условията, предписани от процедурата за изпитване.
Тестовете за надеждност се провеждат като набор от мерки за определяне на показателите за надеждност на етапите на производство и проектиране, както и за контрол на надеждността на разработените и произведени ВЕИ (EMS).
Обект на изследване е партида продукти, от която се взема проба.
Има някои проблеми, свързани с тестването на надеждността.
Първо, тези тестове изискват много време и пари; второ, в процеса на тяхното изпълнение се изразходва част от ресурса на продукта; Трето, съществува проблемът с доверието в резултатите от теста.
Тестовете (I) за надеждност, в зависимост от целта на теста, се разделят наопределящи и контролни.
Определящи И за надеждност се извършват, за да се установят показатели за надеждност на продукта. След това тези показатели (на първо място, средното време до отказ, вероятността за безотказна работа за определеното време, степента на отказ, средното време до отказ) се включват в нормативната и техническа документация за продукта.
Правилният избор на параметри, информиращи за състоянието на продукта (работи или не работи) е от голямо значение при провеждането на окончателно И.
Използват се и специални видове тестове за надеждност, като например:
житейски тестове;
ускорени жизнени тестове;
изпитвания за (не)разрушаване под въздействието на определени фактори.
По време на ускорените тестове всичко се прави като при неускорените тестове, но при повишени натоварвания (електрически, термични и т.н.)
При тестовете за разрушаване натоварването се увеличава, докато причини повреда на продукта.
Тестовете се класифицират според редица критерии:
етапи на създаване или експлоатация на обекти;
място и условия (лаборатория, полеви тестове…);
според използваните методи и оборудване (моделиране, пълномащабен експеримент);
по ниво на обекти (компонентни елементи, отделни устройства, системи).
Резултатите от дефинирането на И са представени като:
статистика на отказите на тествани обекти;
набори от стойности на изходни параметри на обекти;
характеристики на наблюдаваните промени във физичните и химичните процеси в материалите на обектите.
6.2. Окончателни тестове за надеждност
Тези тестове, чиято цел е да се определят показателите за надеждност, могат да се извършват по различни планове.
Тестовият план (I) включва:
брой (N) на обекти, зададени на И;
индикация за броя на обектите, които трябва да бъдат заменени или възстановени в процеса И (U- обектите не се възстановяват и не се заменят;R- обектите, които трябва да бъдат заменени в случай на повреда;M- броят на обектите, които трябва да бъдат възстановени);
броя на отказитеr, до натрупването на които И продължават;
предварително определено времеTизвършване на И;
Така че планът [NUT] предписва извършване на И през времетоTNобекти, без да ги заменя/възстановява. План [NUr] се различава от предишния по това, че И се изпълнява до натрупване наrоткази.
Най-пълната информация се дава от плана [NUN], според койтоNобекта (продукта) се тестват без тяхната подмяна / възстановяване до отказ на всеки от тях. Тук се разкрива цялата емпирична картина на разпределението на отказите във времето. ЗадачаНамирането на показатели за надеждност се решава най-точно и пълно с познаването на закона за разпределение на времето за работа на продуктите до повреда.
Да приемем, че има много наблюдения на непрекъсната случайна променлива (CV), която при тестване на надеждността е времето за отказ на един от многото продукти в тестовата партида. Законът за разпределение на това SW в първо приближение може да се установи от статистическа серия, построена на базата на събрания експериментален материал.
Избор и проверка на хипотезата за закона за разпределение.
Хистограмата , изградена на базата на статистическата серия, дава възможност да се изложи хипотеза за закона на разпределението и след това да се оцени степента на съгласуваност между теоретичното и статистическото разпределение.
2. Изграждане на хистограма
2.1. Според коригираните резултати от теста, т.е. според реалните резултати (с приспадане на системната грешка) се изгражда вариационна серия - подредена извадка. Резултатите в такава серия са подредени във възходящ ред на техните числени стойности.
Приложено към задачата за обработка на статистиката за времето на работа на обектите, вариационният ред се изгражда по естествен начин - по реда на възникване на отказите.
2.2. Тази серия е разделена на определен брой N интервали за групиране на експериментални резултати, като интервалите са с еднаква ширина.h. Числото N трябва да бъде оптимално по отношение на достатъчна изразителност и защита от неравномерни колебания.
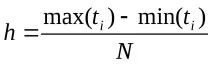
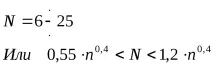
С броя на резултатите от измерването (брой повреди) n≈ 150
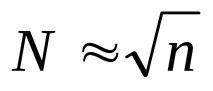
2.3. Броят на стойностите mk на резултатите за всеки k-ти интервал (бит) се преброява, т.е.. определят се абсолютните честотичестоти
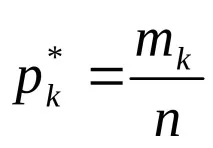
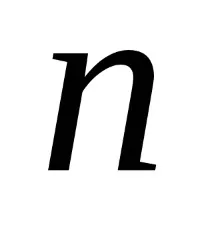
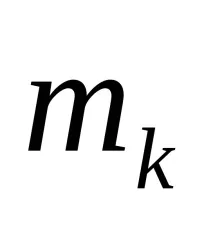
2.4. Изгражда се хистограма. Интервалите на наблюдаваните стойности на SW са нанесени по оста на резултатите, а честотите са нанесени по ординатната ос.
Върху всяка основа с ширина h е изграден правоъгълник с височина
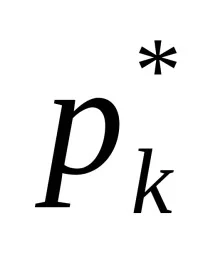
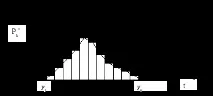
Ординатите, пропорционални на честотите, реконструирани в средата на колоните, перпендикулярни на абсцисната ос, позволяват да се построи многоъгълник (фиг. 1). Сравнението на полигона, получен въз основа на събраната статистика с различни криви на плътност на разпределението, ще позволи да се изложи хипотеза за закона на разпределението. След това е необходимо да се оцени степента, в която експерименталните данни са в съответствие с тази хипотеза.
2.5. Когато броят на наблюденията е повече от 50, тестът на Pearson (най-често използваният тест за съответствие) се използва за проверка на правдоподобността на предложената хипотеза за закона за разпределение.
За да направите това, трябва да имате статистическа серия:
За хипотетично разпределение се намират теоретичните вероятности:
Мярка
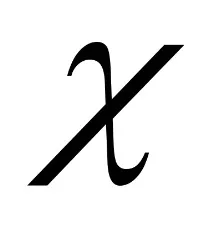
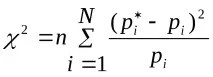
Тук
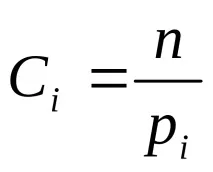
Въведената мярка χ 2 е RV, която има разпределението на Пиърсън с броя на степените на свобода r = N – 1 – ν, където ν е броят на параметрите, които еднозначно определят този закон на разпределение.
Съставени са таблици със стойности на χ 2 за различни нива на значимост q = 1 – Pdf, където Pdf е нивото на достоверност, с което се приема хипотезата за закона за разпределение (таблица - в прил.). Ако мярката, изчислена от експерименталните данни, е мяркаχ 2 2 )q, тогава с вероятност q се приема хипотезата за закона на разпределението.
В моментавреме за тестване на хипотезата, се приема двустранна критична област, т.е. хипотезата се приема, ако
При познаване на закона за разпределение показателите за надеждност могат да бъдат изчислени въз основа на доста ограничен набор от експериментални данни. Това се илюстрира със следния пример.
Пример. При тестването на 100 продукта за ti = 200 h са регистрирани откази на 2 продукта. Определете средното време T1 на времето до повреда, ако е известно, че произволното време на повреда на продукта се подчинява на експоненциален закон.
Вероятността за повреда се изчислява по формулата
.
Според резултатите от И статистическата стойност на Q е 0,02.
;
където t = ti = 200 h.
Получаваме
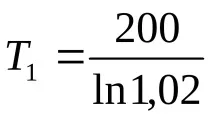
Ако в резултат на проведеното И се получи поредица от стойностиti(случайни стойности на времето на отказ), точковите оценки на мат. очакванията и дисперсиите на средното време до отказT1се намират по формулите:
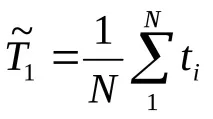
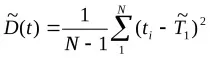
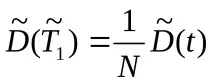
Всяка точкова оценка, получена въз основа на тестове, има съществения недостатък, че самата тя е случайна променлива. Следователно, за точковите оценки е необходимо да се намерят доверителни интервали, в които те попадат с доверителна вероятност β.
Показателно в това отношение е намирането на доверителния интервал за средното време между отказите.
Нека разгледаме най-простия поток на отказ на Поасон на RES (EMS). Вероятността за поява наkповреди по време на tΣ в съответствие със закона на Поасон ще бъде
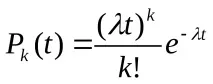
Вероятността за работа с брой повреди ≤rсе изчислява съгласно (6.6) като
. (6,7)
Изразът (6.7) съответства на интегралната функция на разпределението χ 2 на случайната променливаtΣ до появата наrоткази. Същинското χ 2 -разпределение с ν = 2r степени на свобода се подчинява на случайната променлива
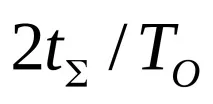
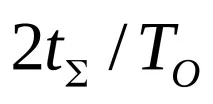
. (6,8)
Диференцирането на тази функция по отношение на dχ 2 дава функцията на плътността на разпределението (фиг. ). Двустранната критична област се приема като доверителен интервал за дадена доверителна вероятност β
Тогава стойносттаTОе в доверителния интервал
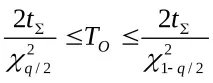
Стойностите на мярката χ 2 в зависимост от нивото на значимост q и броя на степените на свобода ν са дадени в таблица №.
р