6.4.1. Ортогонални планове от втори ред
Като цяло тази матрица е неортогонална, т.к
(6,27)
Привеждаме матрицата в ортогонална форма, за която въвеждаме нови променливи (трансформации за квадратични ефекти)
При което
Тогава регресионното уравнение (модел на процеса) ще бъде написано като
Композиционните планове могат лесно да бъдат сведени до ортогонални, като се избере звездното рамо a. В табл. 6.9 показва стойността на a за различен брой фактори k и броя на експериментите в центъра на плана n0.
Таблица 6.9
| Брой експерименти | Звездообразно рамо a за различен брой фактори k | ||
| в центъра на плана, n0 | k=2 | k=3 | k=4 |
| 1 | 1,00 | 1.22 | 1.41 |
| 2 | 1.08 | 1.29 | 1.47 |
| 3 | 1.15 | 1.35 | 1.55 |
| 4 | 1.21 | 1.41 | 1.61 |
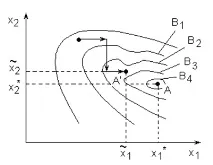
По-специално, ортогоналният дизайн от втори ред за k=2 и n0=1 е представен в таблица. 6.10, и неговата геометрична интерпретация на фиг. 6.3a.
Представен на фиг.6.3а и табл. 6.10, правоъгълен (квадратен) експериментален план за модел от втори ред е приложим, макар и донякъде излишен (9 експеримента за определяне на 6 коефициента). Благодарение на три излишни експеримента, това ни позволява да осредним случайните грешки и да оценим тяхното естество.
Ортогонален план от втори ред
| Номер | Фабрика | Резултат | |||||
| опит | x0 | x1 | x2 | x1x2 | x1' | x2' | yi |
| 1 | +1 | -1 | -1 | +1 | +1/3 | +1/3 | y1 |
| Ядро 2 | +1 | +1 | -1 | -1 | +1/3 | +1/3 | y2 |
| план 3 | +1 | -1 | +1 | -1 | +1/3 | +1/3 | y3 |
| 4 | +1 | +1 | +1 | +1 | +1/3 | +1/3 | y4 |
| 5 | +1 | а=+1 | 0 | 0 | +1/3 | -2/3 | y5 |
| Звезди - 6 | +1 | а=-1 | 0 | 0 | +1/3 | -2/3 | y6 |
| 7 | +1 | 0 | а=+1 | 0 | -2/3 | +1/3 | y7 |
| точки 8 | +1 | 0 | а=-1 | 0 | -2/3 | +1/3 | y8 |
| Център 9 |
план
В тази таблица
а - ортогонален; b - въртящ се
Поради ортогоналността на планиращата матрица, всички коефициенти на регресионното уравнение b се определят независимо един от друг по формулата:
(6,28)
Тук i е номерът на колоната в плановата матрица; j е номерът на реда; сумата е различна за линейни, квадратични ефекти и взаимодействия.
Дисперсиите на коефициентите на регресионното уравнение са
(6,29)
Специално трябва да се отбележи, че коефициентите на регресионното уравнение, получени с помощта на ортогонални планове от втори ред, се определят с различна точност (виж уравнение 6. ), докато ортогоналните планове от първи ред осигуряват същата точност на коефициентите, т.е. въпреки че дизайн 6. е ортогонален и осигурява независимостта на определяне на коефициентите b, той не може да се върти!
В резултат на изчисления върху матрица с трансформирани колони за квадратични ефекти, получаваме уравнение във формата
(6,30)
За да се преобразува в обичайната нотация, трябва да се премине от коефициента b0' към коефициентаb0 с помощта на израза
(6,31)
В този случай дисперсията на този коефициент се изчислява по следната зависимост
(6,32)
В бъдеще, като се знае дисперсията на възпроизводимостта, се проверяват значимостта на коефициентите и адекватността на уравнението:
(6,33)
Значимостта на коефициентите се проверява чрез t-критерия на Стюдънт
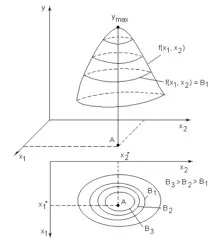
Адекватността на уравнението се проверява чрез критерия на Фишер