§8. Изображение на повърхности на въртене и полиедри в чертежа
Повърхнини и тела на въртене.
Такива повърхности се образуват чрез въртене на образуваща (права линия или плоска крива) около фиксирана ос.Фиг.1.64показва чертеж на повърхност, получена чрез въртене на образуващата ABSD около оста J.
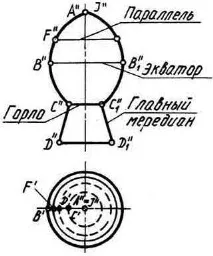
За удобство на изображението на чертежа повърхността на въртене е показана с ос, разположена перпендикулярно на една от проекционните равнини.
При въртене всяка точка от генератора описва окръжност, чиято равнина е перпендикулярна на оста. Тези кръгове се наричат паралели. Най-големият от паралелите се нарича екватор (нафиг.1.64- паралел В"В"1), най-малкият - гърло (нафиг.1.64- паралел С"С"1). Равнината, минаваща през оста на повърхността на въртене, се нарича меридионална, а линията на пресичане на повърхността с тази равнина се нарича меридиан. Меридианът, проектиран върху равнината на проекцията без изкривяване, се нарича главен меридиан. Повърхността на въртене на чертежа обикновено се показва на една от проекционните равнини чрез проекцията на главния меридиан, на другата равнина - чрез проекцията на екватора. Оста на въртене на повърхността е показана с пунктирана тънка линия.
Известно от училищния курс по повърхностна геометрия: цилиндър на въртене и конус на въртене са специални случаи на разглежданите повърхности. За цилиндър и конус на въртене меридианите са успоредни или пресичащи се прави линии. На чертежа безкрайните праволинейни генератори са ограничени от паралели (базиси), т.е. тези повърхности са изобразени като прав кръгов цилиндър и прав кръгов конус. В този случай една от основите на цилиндъра или основата на конуса е подравнена с равнината на проекцията (Фиг.1.65).
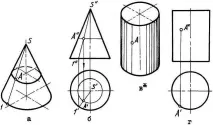
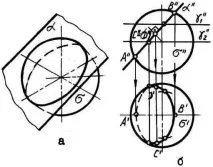
Сферична повърхност се образува чрез завъртане на кръг около един от диаметрите. Напроекционни равнини сферата е изобразена като кръгове с еднакъв диаметър (фиг.1.66).
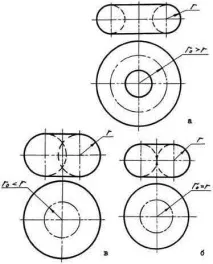
Когато окръжност или дъга от окръжност се върти около ос, която лежи в равнината на тази окръжност, но не минава през нейния център, се образува повърхност - тор. Нафиг.1.67са показани повърхнини: a - отворен тор, b - затворен тор, c - самопресичащ се тор.
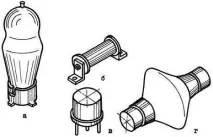
Телата, ограничени от повърхности на въртене, се използват широко в инженерството.Фиг.1.68показва продукти, съдържащи тези повърхности:
- а - електронна лампа;
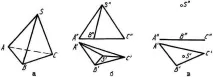
Ние се ограничаваме до разглеждане на призматични и пирамидални полиедри. Повърхностите на призмата и пирамидата са поредица от плоски лица, пресичащи се помежду си по прави линии (ръбове), които от своя страна се пресичат в точки (върхове). Тези. изображението на чертежа на многостен се свежда до изображение на поредица от сегменти и точки (Фиг.1.69,Фиг.1.70).
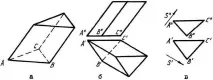
Призматична повърхност може да бъде определена на чертежа чрез проекции на фигура, получена чрез пресичане на повърхността с равнина и проекции на ръбове или тяхната посока (Фиг.1.69c).
Пирамидалната повърхнина може да бъде определена и чрез фигурата на сечението на страничните ребра от равнината (основата) и точката на пресичане на ребрата - от върха (Фиг.1.70c).
По-често на чертежа е изобразена призма, т.е. част от призматична повърхност, ограничена от две успоредни равнини, основите. Препоръчително е да поставите основите на призмата успоредно на равнината на проекциите (Фиг.1.69b). Когато се изобразява пирамида, нейната основа се поставя успоредно на равнината на проекциите или лежи в тази равнина (Фиг.1.70b).