9.1. Вероятностни източници на съобщения.
В тези модели източникът на обикновен текст се третира като източник на произволни последователности. Смята се, че източникът генерира крайна или безкрайна последователност от произволни знаци x(1),x(2),…,x(n) от азбуката I. Вероятността за произволно съобщение „i(1),i(2),…, i(n)“ се определя като вероятността от съвместно събитие
В този случай, разбира се, трябва да бъдат изпълнени следните условия:
за произволно съобщение "i(1),i(2),…, i(n)"
2)=1;
3) за произволно съобщение "i(1),i(2),…, i(n)"
Р(i(1),i(2),…, i(n))=,sn+1.
Значението на последното условие е, че вероятността за произволно съобщение с дължина n е сумата от вероятностите на всички "продължения" на това съобщение до дължина s> n (някаква версия на аксиомата на Колмогоров). Текстът, генериран от такъв източник, е вероятностен аналог на език. Той има същите честотни характеристики на k-грами като езика. Чрез задаване на конкретно разпределение на вероятностите върху набора от обикновени текстове, ние задаваме съответния модел на източника на съобщение. Нека разгледаме някои специални случаи на този общ модел.
Стационарен източник на независими знаци от азбуката.Този модел предполага, че вероятностите на съобщенията са напълно определени от вероятностите на отделните знаци от азбуката:
P(i(1),i(2),...,i(n))=
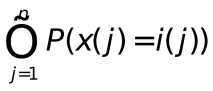
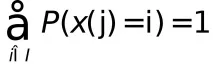
Подв обикновен текстсе разбира прилагането на последователност от независими опити в полиномиална вероятностна схема с брой резултати I=m.Резултатът е съответствие едно към едно със символа на азбуката I. Този модел ни позволява да разделим буквите от азбуката на класове с висока, средна и ниска честота на използване. По-долу са буквите с висока честота на употреба за някои европейски езици (честотапосочено като процент).