Абсорбция, слепване и теореми на де Морган
Теоремата за поглъщане е написана в две форми - дизюнктивна и
Нека докажем първата теорема. Нека извадим буквата А от скобите:
A+ AB= A(1 + B)
Съгласно теорема (3) 1 +В = 1, следователно
За да докажем втората теорема, разширяваме скобите:
A(A + B) = A • A + AB = A + AB
Резултатът е израз, който току-що е доказан.
Нека разгледаме няколко примера за приложението на теоремата за абсорбция за
опростяване на булеви формули.
Теоремата за слепване също има две форми — дизюнктивна и
Нека докажем първата теорема:
тъй като съгласно теореми (5) и (4)
За да докажем втората теорема, отваряме скобите:
Съгласно теорема (6), следователно:
Съгласно теоремата за абсорбция (16)A+AB = A
Теоремата за поглъщане, подобно на теоремата за слепване, се прилага при опростяване
булеви формули, например:
Теоремата на Де Морган свързва трите основни операции на булевата алгебра
дизюнкция, конюнкция и инверсия:
Първата теорема гласи следното: инверсията на конюнкция е дизюнкция
инверсии. Второ, инверсията на дизюнкция е конюнкция на инверсии. Можете да докажете теоремите на Морган, като използвате таблици на истината за лявата и дясната страна.
Теоремата на Де Морган също се прилага за повече променливи:
Лекция 5
Инвертиране на сложни изрази
Теоремата на Де Морган се прилага не само за единични връзки
или дизюнкции, но и до по-сложни изрази.
Нека намерим инверсията на изразаAB + CD,представен като дизюнкция на съюзи. Инверсията ще се счита за завършена, ако отрицателните знаци са само над променливите. Нека въведем обозначението:AB = X;
Да намерим инека заместим в израз (22):
Помислете за израз, представен в конюнктивна форма:
(A + B)(C + D)
Нека намерим неговата инверсия във формата
Нека въведем обозначението:A + B = X; C + D =Y,след това
Намерете ги и ги заменете в израза
Когато обръщате сложни изрази, можете да използвате следното правило. За да намерите инверсията, е необходимо да замените знаците за конюнкция с знаци за дизюнкция, а знаците за дизюнкция с знаци за конюнкция и да поставите инверсии над всяка променлива:
Концепцията за булева функция
В общо, функция
картографиране) е определено правило (закон), според което всеки елемент от множествотоX,, което е обхватът от стойности на независимата променливах,, се свързва с определен елемент от множествотоF,
което се разбира като диапазон от стойности на зависимата променливаf. В случай на булеви функцииX = F = . Правилото, по което се определя функцията, може да бъде всяка булева формула, например:
Символътf тук обозначава функция, която, подобно на аргументите A,B, C,, е двоична променлива.
Аргументите са независими променливи, те могат да приемат всякаква стойност - 0 или 1. Функциятаf е зависима променлива. Значението му се определя изцяло от стойностите на променливите и логическите връзки между тях.
Основната характеристика на функцията е, че за да се определи нейната стойност, в общия случай е необходимо да се знаят стойностите на всички аргументи, от които тя зависи. Например горната функция зависи от три аргумента A,B, C.Ако вземем A = 1, получаваме
т.е. получава се нов израз, който не е равен на нула,нито едно
мерна единица. Сега некаB= 1. Тогава
т.е. в този случай не е известно дали функцията е равна на нула или единица.
Нека накрая приемемС= 0. Тогава получаваме:f=0. Така, ако в оригиналния израз приемем A = 1,B= 1,C=0, тогава функцията ще приеме нулева стойност:f = 0.
Разгледайтеконцепцията за набор от променливи стойности.
Ако на всички аргументи, от които зависи функцията, са присвоени определени стойности, тогава се говори за набор от стойности на аргументи, които могат да бъдат
просто го наречете набор. Наборът от стойности на аргументи е поредица от нули и единици, като например 110, където първата цифра съответства на първия аргумент, втората на втория и третата на третия. Очевидно е необходимо предварително да се договорим какъв е първият, вторият или, да речем, петият аргумент. За да направите това, е удобно да използвате азбучното подреждане на буквите.
Например ако
тогава, според латинската азбука, първият аргумент еP, вторият -
Q, трето -X, четвърто - Y. След това чрез набора от стойности на аргументи е лесно
намерете стойността на функцията. Нека например е дадено множеството 1001. Според него
записи, т.е. на набор 1001 дадената функция е равна на единица.
Обърнете внимание отново, че наборът от стойности на аргументи е наборът
нули и единици. Двоичните числа също са набори от нули и единици.
Това повдига въпроса - могат ли множествата да се разглеждат като двоични
числа? Възможно е и в много случаи е много удобно, особено ако двоичният файл
преобразувайте числото в десетична. Например ако
A = 0, B = 1, C = 1,D=0,
тогава наборът ще приеме формата 0110. Ако се счита за двоично число, тогава:
т.е. даден наборима числото 6 в десетичен знак.
Ако искате да намерите стойностите на аргументите по десетично число, тогава
действаме в обратен ред: първо превеждаме десетичното число в двоично, след това добавяме толкова нули отляво, така че общият брой цифри да е равен на броя на аргументите, след което намираме стойностите на аргументите.
Нека, например, е необходимо да се намерят стойностите на аргументите A,B, C, D, E, Fот набора с числото 23. Преобразуваме числото 23 в двоичната система, използвайки метода
В резултат на това получаваме 2310 = 101112. Това е петцифрено число и общо
има шест аргумента, следователно една нула трябва да бъде написана отляво:
2310 = 0101112. От тук намираме:
A = 0, B = 1, C = 0, D = 1, E = 1, F = 1.
Колко набора има, ако е известен броят наn аргумента? Очевидно толкова, колкото има n-битови двоични числа, т.е. 2 n
Лекция 6
Дефиниция на булева функция
Вече знаем един начин. Той е аналитичен, тоест под формата на математически израз, използващ двоични променливи и логически операции. В допълнение към него има и други начини, най-важният от които е табличният. В таблицата са изброени всички възможни набори от стойности на аргументи, като за всеки набор е посочена стойността на функцията. Такава таблица се нарича таблица на съответствие (истина).
На примера на функцията
Нека да разберем как да изградим справочна таблица за него.
Функцията зависи от три аргументаA, B, C. Следователно в таблицата
предоставяме три колони за аргументите A,B,C и една колона за стойностите на функцията f. Отляво на колона А е полезно да поставите друга колона. В него ще записваме десетични числа, които съответстват на множества, ако ги считаме затрицифрени двоични числа. Този десетичен знак
колоната е въведена за удобство при работа с таблицата, следователно по принцип,
може да се пренебрегне.
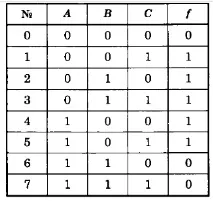
Попълваме таблицата. Редът с номера на LLC гласи:
A = B = C = 0.
Нека дефинираме стойността на функцията в този набор:
В колона f записваме нула в реда с набор 000.
Следващ набор: 001, така чеe. A = B = 0, C = 1. Намерете стойността на функцията
На набор 001 функцията е равна на 1, следователно в колона f в реда с
номер 001 записваме единицата.
По същия начин изчисляваме стойностите на функциите на всички други набори и