Алгебра, ръчна математика

Любителска математика - направи си сам

Предизвикателство за първокурсници

Кратък предговор

Вчера Саша Т ми зададе гатанка, която, както каза, един от неговите първокурсници разгадал за четири дни. Не знам дали да се срамувам или не, че такъв обрасъл зашеметител като мен не го реши моментално, но въпреки това тази сутрин намерих решение.

Намирам . (Когато гадаете, можете да намигнете лукаво и да направите двусмислена забележка, че казват, че това е функция „не математическа, а като в програмирането.“)

Първото нещо, което идва на ум, е брилянтна идея, че, но уви, функцията, по условие, трябва да преобразува цели числа в цели числа.

Втората брилянтна идея е да се създаде нещо като в добрите стари времена, а именно да се вземе функция от двете страни на определящото уравнение:

което символизира, че желаната функция е странна, и по-специално . Доста математически, така че :)

Третата брилянтна идея, след агонизиращото изкушение да се впуснем в доказателство, че такава функция не съществува, беше да пренапишем конститутивното уравнение, както следва:

и възкликнете „Еврика! Да, това е функция, която за нея е обратна!

След това трябва да помислите за графиката на тази функция. Графиката от графиката се получава чрез отражение от абсцисната ос, а графиката (която, в съответствие с пренаписаното определящо уравнение, съществува сама за себе си) се получава от графиката чрез отражение от ъглополовящата на първия квадрант. Нашата функция е забележителна с това, че и двете от тези отражения дават едно и също нещо: , където е графиката на и са нашите отражения. Следователно и тъй като има идентично картографиране, тогаваграфиката е инвариантна по отношение на състава на двете горни отражения.Съставът на две отражения по отношение на линиите е завъртане под ъгъл, равен на два пъти ъгъла между осите на симетрия около пресечната точка на осите. В нашия случай това е просто завъртане под прав ъгъл около началото.

И така, графиката на желаната функция е инвариантна по отношение на завъртанията през прав ъгъл около началото (лесно е да се разбере, че няма значение дали да се правят завъртания по посока на часовниковата стрелка или обратно на часовниковата стрелка). Тогава трябваше да си спомня конвулсивно как тези завои се записват в координатите :) Точката отива към .

Така че на графиката на функцията, заедно с точката, определено ще има точки , , . След това дори трябваше да взема парче карирана хартия и да започна да мушкам точки, казвайки нещо като: „И така, след това вземаме , тогава трябва да бъде , и в лявата полуравнина продължаваме странно.“ След препятствия, картината се появи и решението беше написано:

Означаваме , тогава и по същия начин , . Избираме безкрайно правилно подмножество и дефинираме произволна биекция (тя трябва да съществува, тъй като всички безкрайни подмножества на естествената серия са еквивалентни). Дефинираме желаната функция като

Освен това е очевидно от всички предходни разсъждения, че всички желани функции трябва да имат точно тази форма.

Кратък послеслов

Оказа се, че функцията се оказва съвсем математическа, а не програмистка и процесът на отгатването й мобилизира много зони от бързо намаляващия ми мозък, за което съм изключително благодарен на целия екип на PAYcast.

Разпределителни решетки

Определение

Решетката се нарича разпределителна, ако е в сила един от следните закони:

Еквивалентност на два закона за дистрибутивност

Нека е вярно това, тогава добавете от двете страни:

Тук сме използвали единот законите на абсорбцията. Сега нека заместим в оригиналния закон за разпределение вместо:

Сравнявайки последните редове в тези две изчисления (във второто използвахме различен закон за абсорбция), заключаваме, че

По подобен начин (променяйки се на и обратно), получаваме доказателство, че полученият закон за разпределение може да се използва за извеждане на оригиналния, използвайки законите за абсорбция, асоциативност и комутативност на операциите.

Примери за разпределителни решетки

Най-простият пример са различните подрешетки на решетката на всички подмножества на определено множество, по-специално решетките на отворени и затворени множества на произволно топологично пространство, двойствено едно към друго (изоморфизъм на двойствеността - приемане на допълнението към цялото пространство).

Пример за неразпределителна решетка

Разгледайте следната диаграма на Хасе:

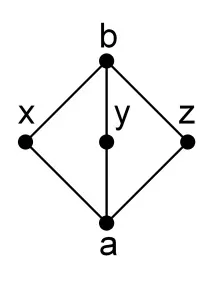
Очевидно е, че тази диаграма дефинира решетка и че , и . Всъщност повечето наистина интересни решетки не са разпределителни.

Неравенство на разпределението

Законът за дистрибутивност под формата на равенство е изпълнен, най-общо казано, не във всички решетки. Въпреки това, може да се види, че в произволна решетка , и следователно . Освен това, което означава. Това означава, че в произволна решетка е валидно следното неравенство:

Решетъчен изоморфизъм, подрешетки и идеали

Дефиниции

Две решетки и са изоморфни, ако съществува едно-към-едно съответствие, така че

Подмножество на решетка се нарича подрешетка, ако е затворено за операциите и .

Подмножество на решетка се нарича долен сегмент, ако удовлетворява свойството

Непразен долен сегмент на решетката се нарича идеал, ако е затворен при операцията .

Теорема за изоморфизъм

Въпреки факта, че всички дефиниции са напълно стандартни, решетъчните изоморфизми имат някои доста добри свойства. Ще приемем, че отношенията на частичен ред са дадени върху решетките по обичайния начин. Преобразуване на две частично подредени множества се нарича монотонно, ако запазва реда между елементите. Сега самата формулировка:

Теорема. Биекция между решетки и е изоморфизъм тогава и само ако и са монотонни преобразувания.

Доказателство.

Нека биекцията е изоморфизъм. Тогава, ако , Тогава, по дефиницията на връзката на реда, , И следователно . По същия начин от получаваме .
Нека и са монотонни преобразувания. Тогава и , и следователно , т.е. е долната граница на . Да предположим, че тази долна граница не е точна, т.е. съществува някои , Тогава, поради монотонността на , , Откъдето и , Това е, и следователно . По подобен начин се доказва, че , което завършва доказателството, че е изоморфизъм.

Друга дефиниция на долния сегмент

Дефиницията на долния сегмент, дадена по-горе, изглежда като дефиниция на "недо-идеален" и името "долен сегмент" изглежда неоправдано. Всъщност, ако е долният сегмент на решетката , и , тогава , и следователно . Тоест долният сегмент, заедно с който и да е от неговите елементи, съдържа всички елементи на решетката, които са по-малки от него. Обратно, ако някакво подмножество на решетката съдържа, заедно с всеки от нейните елементи, който и да е от нейните по-малки елементи, тогава ние вземаме всеки и разглеждаме , тогава , тоест е долният сегмент на решетката в нашата дефиниция.

Решетка на долния сегмент

Долните сегменти могат да бъдат разграничени не само в решетки, но и в произволни частично подредени множества. Ако вземем два долни сегмента на някои частично подреден набор , тогава ако и , тогаваили (тогава) или (тогава отново). Ако, тогава, което означава. От друга страна, което означава обща сума, . Оказва се, че пресечната точка и обединението на двата долни сегмента е долният сегмент. От свойствата на обединение и пресичане заключаваме, че множеството от всички долни сегменти на произволно частично подредено множество образува решетка.

Между другото, формално празният набор също е долният сегмент. Множеството от всички непразни долни сегменти на частично подредено множество се обозначава и е решетка, ако има най-малък елемент в (в този случай всеки непразен долен сегмент ще съдържа най-малкия елемент и пресечната точка на два непразни долни сегмента също ще бъде непразно).

Основни идеали

Основният идеал на решетката, генериран от елемента, се нарича множество. Очевидно това е най-ниският сегмент. Действително, ако , a , тогава , това е . Също така, ако , Тогава и , Това е . Освен това . Това означава, че основният идеал в нашата дефиниция наистина е идеал. Освен това може да се дефинира главният идеал по алгебричен начин. Всеки елемент от основния идеал има свойството , и следователно . Означава, че .

Решетка от идеали

Ако вземем два идеала, тогава тяхното пресичане също очевидно е идеал (доказателството, че е затворено при операции, е толкова скучно, колкото и за долните сегменти). Пресечната точка на два идеала не е празна, защото , , което означава, че .

Като цяло е съвсем очевидно, че наборът от идеали, подреден от теоретико-множественото включване, е решетка, въпреки че като цяло втората операция (не пресичане) изглежда като нещо доста епично.

Подрешетка на главните идеали

За главните идеали операциите в решетката на всички идеали могат да бъдатда бъдат изразени по много прост начин чрез операции върху родителски елементи.

Да разгледаме два основни идеала и и някакъв елемент, принадлежащ на тяхното пресичане. Тогава от едната страна, а от другата, тогава. Обратно, ако , Тогава , Това е и и по същия начин . Това доказва, че.

Сега помислете за някакъв елемент, принадлежащ на . Нека , тогава , и следователно . По същия начин, ако , тогава . Това означава, че идеалът е горната граница (чрез отношението на вграждане на множества) на двойката. Нека докажем, че тази граница е точна. Нека и да бъде идеал. Тогава по-специално. Въпреки това, ако , тогава , откъдето веднага , и . Тоест идеалът е най-малката горна граница на двойката.

По този начин главните идеали образуват подрешетка в решетката на всички идеали. И нещо повече, което е най-любопитно, решетката на главните идеали е изоморфна на оригиналната решетка ( ).

Решетки. Определения и примери

Две дефиниции на решетките

От една страна, решетката е алгебрична система " title="\left " class="latex" /> с две операции, отговарящи на следните свойства:

(комутативност на операциите)
(асоциативност на операциите)
(закони на абсорбцията)

От друга страна, решетката е частично подредено множество " title="\left " class="latex" />, в което за всяка двойка елементи са дефинирани нейните точни горна и долна граница ( и ).

Еквивалентност на определенията

Лесно е да се види, че ако решетката е дадена чрез операции, тогава е възможно да се въведе връзка на ред върху нея, която ще удовлетвори свойството от друга дефиниция. По същия начин, ако решетката е дадена като частично подредено множество, тогава операциите върху нея могат да бъдат въведени като . Ако, действайки според тези рецепти, първо получим връзка от операции и след това отново получим от получената връзкаоперации, тогава стигаме до оригиналните операции (по подобен начин, ако започнем с релация).

Директно следване. Диаграми на Хасе

На всяка решетка, както и на частично подредено множество, може да се дефинира друга връзка, наречена непосредствена последователност (разчетена като „следва непосредствено след“). Тази връзка ще бъде рефлексивна и антисиметрична, но няма да бъде транзитивна и следователно няма да бъде връзка на ред или дори на предпорядък. Диаграмата на Хасе е графика на директна следствена връзка, по която е лесно (чрез транзитивно затваряне) да се възстанови първоначалната релация на ред върху решетката.

Двойна решетка

В първата дефиниция на решетката е лесно да се види, че ако двете операции се разменят, тогава аксиомите все още ще са валидни. Решетка, получена чрез замяна с и обратно, се нарича двойствена към дадената. Диаграмата на Хасе на двойната решетка се получава чрез обръщане на посоките на стрелките.

Системата от подмножества на произволно множество по отношение на операциите обединение и пресичане (частичен ред - чрез влагане);
множеството от естествени числа по отношение на операциите за намиране на най-голям общ делител и най-малко общо кратно (частичен ред - делимост);
система от подгрупи на произволна група по отношение на операциите пресичане и умножение (частичен ред чрез влагане);
система от подмодули на произволен модул по отношение на пресичане и добавяне, по-специално система от идеали на произволен асоциативен пръстен или система от подпространства на векторно пространство (частичен ред чрез вграждане);
всяко линейно подредено множество, по-специално всяко подмножество на множеството от реални числа по отношение на операциите за намиранемаксимум и минимум на двойка числа;
множеството от непрекъснати функции с реални стойности върху компактно множество по отношение на операциите на точков максимум и минимум на функции (частичен ред - точково).

Идемпотентност

Ако заместим в закона за поглъщане, прилагайки втория закон за поглъщане, получаваме . По същия начин се установява, че. Понякога тези свойства са включени в набора от решетъчни аксиоми.

Групов център

След като засега гръм падна върху теоремата на Хурвиц от огромна височина, защо не публикувате нещо просто.

Нека разгледаме група. Тогава вътрешен автоморфизъм е трансформация на група в себе си, така че . От тук е лесно да се види това. По този начин множеството от всички вътрешни автоморфизми в групата на всички трансформации на групата в себе си съставлява подгрупа. Тези трансформации са наистина автоморфизми, тъй като . Освен това, тъй като чрез това, което беше доказано по-горе, картографирането, което свързва елемент от група с елемент от група (както се обозначава групата от вътрешни автоморфизми), само по себе си е хомоморфизъм на групи. Да намерим.

Ядрото на дисплея са елементите, които влизат в трансформацията на идентичността на групата. Ако , тогава , т.е. елементът комутира с всички елементи на групата . Елементите, които комутират с всички елементи от определена група, се наричат център на тази група. Току-що доказахме, че центърът е ядрото на някакъв групов хомоморфизъм. Както е известно, ядрото на хомоморфизъм на група е нейната нормална подгрупа, . От същото общо твърдение за структурата на хомоморфизма получаваме, че . Това означава по-специално, че. В случай на абелеви групи, вътрешната група автоморфизми също е тривиална. В случай на неабелеви групи, дели . Също така е лесно да се види от определението за център на група, че самият център е винагиабелева група.