Алгебрична теория на графите
Алгебричната теория на графитее клон на математиката, който прилага алгебрични методи за графични проблеми. Други подходи към проблеми с графики са геометрични, комбинаторни и алгоритмични. Има три основни клона на алгебричната теория на графите - два клона използват линейна алгебра и теория на групите, а един клон изучава инвариантите на графите.
Съдържание
Използване на линейна алгебра
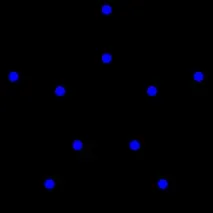
Първият клон на алгебричната теория на графите изучава графики с помощта на линейна алгебра. По-специално, той изучава спектрите на матрицата на съседство или матрицата на Кирхоф на граф (тази част от алгебричната теория на графите се нарича също спектрална теория на графите). За графиката на Петерсен, например, спектърът на съседната матрица е (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Някои теореми свързват свойствата на спектъра с други инварианти на графиката. Като прост пример, свързан график с диаметърDще има понеD+1 различни стойности в своя спектър [1] . Свойствата на спектъра на графиката се използват за анализ на синхронността на мрежата [en] .
Използване на теория на групите
Този втори клон на алгебричната теория на графите е свързан с първия, тъй като свойствата на симетрия на графиката се отразяват в нейния спектър. По-специално, спектърът на графика с висока симетрия, като графиката на Петерсен, има няколко различни собствени стойности [1] (графиката на Петерсен има 3 стойности, което е най-малкото възможно число за графика с диаметър като графиката на Петерсен). За графиките на Кейли спектърът може да бъде пряко свързан със структурата на групата, по-специално с нейните несводими представяния [1] [3] .
Изследване на инварианти на графики
И накрая, третият клон на алгебричната теория на графите се занимава с алгебрични свойстваграфични инварианти, по-специално с хроматични полиноми, полиноми на Тата [en] и инварианти на възли. Хроматичният полином на графика, например, отчита броя на нейните правилни оцветявания на върховете. За графиката на Петерсен този полином е t ( t − 1 ) ( t − 2 ) ( t 7 − 12 t 6 + 67 t 5 − 230 t 4 + 529 t 3 − 814 t 2 + 775 t − 352 ) -12t^+67t^-230t^+529t^-814t^+77 5t-352)& gt; [1] . По-специално, това означава, че графиката на Петерсен не може да бъде правилно оцветена с един или два цвята, но с три цвята тя може да бъде оцветена по 120 различни начина. Много работа в тази област на алгебричната теория на графиките беше причинена от опитите да се докаже теоремата за четирите цвята. Въпреки това остават много отворени въпроси, като например определяне кои графики имат един и същ хроматичен полином и кои полиноми са хроматични.