Аналитична геометрия в пространството

$d=\sqrt$

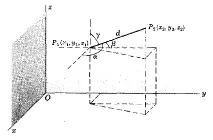
ПОСОЧЕН КОСИНУС НА ЛИНИЯТА, СЪВЪРЗВАЩА $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$$l=\cos\alpha=\frac$, $m=\cos\beta=\frac$, $n=\cos\gamma=\frac$

където $\alpha,\beta,\gamma$ са ъглите, които линията $P_1P_2$ сключва съответно с положителните оси $x,y,z$, а $d$ е дефиниран на фигурата по-горе.

СЪОТНОШЕНИЕ МЕЖДУ НАПРАВЛЕНИТЕ КОСИНУСИ$\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$ или $l^2+m^2+n^2=1$

ВОДЕЩИ ЦИФРИЧислата $L,M,N$, които са пропорционални на направляващите косинуси $l,m,n$, се наричат ​​водещи числа. Връзка между тях

Това е валидно и ако $l, m, n$ се ​​заменят съответно с $L, M, N$.

УРАВНЕНИЯ НА ЛИНИЯ, СЪВЪРЗВАЩА $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧНА ФОРМА$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$

Това е валидно и ако $l, m, n$ се ​​заменят съответно с $L, M, N$.

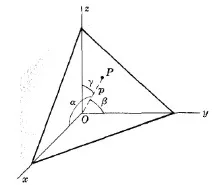
ЪГЪЛ $\phi$ МЕЖДУ ДВЕ ПРАВИ С НАПРАВЛЕН КОСИНУС $l_1, m_1, n_1$ И $l_2, m_2, n_2$$\cos\phi=l_1l_2+m_1m_2+n_1n_2$

ОБЩО УРАВНЕНИЕ НА РАВНИНАТА$Ax + By + Cz + D = 0$ [$A, B, C, D$ са константи]

УРАВНЕНИЕ НА РАВНИНА, ПРЕМИНАВАЩА ПРЕЗ ТОЧКИТЕ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$

$\beginx-x_1 & y-y_1 & z-z_1\\ x_2-x_1 & y_2-y_1 & z_2-z_1\\ x_3-x_1 & y_3-y_1 & z_3-z_1\end=0$

$\begin y_2-y_1 & z_2-z_1\\ y_3-y_1 & z_3-z_1\end(x-x_1)$ $+\begin z_2-z_1 & x_2-x_1\\z_3-z_1 & x_3-x_1\end(y-y_1)$ $+\begin x_2-x_1 & y_2-y_1\\ x_3-x_1 & y_3-y_1\end(z-z_1)=0$

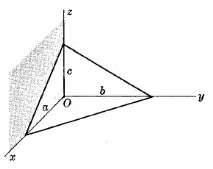
където $a, b, c$ са пресечните точки на осите $x, y, z$, съответно.

Забележка,че водещите числа за правата, перпендикулярна на равнината $Ax + By + Cz + D = 0$, са $A, B, C$.

където знакът е избран така, че разстоянието да не е отрицателно.

НОРМАЛНИ РАВНИНСКИ УРАВНЕНИЯ$x\cos\alpha+y\cos\beta+z\cos\gamma=p$

където $p$ = перпендикулярно разстояние от $O$ до равнината в $P$ и $\alpha, \beta, \gamma$ са ъглите между $OP$ и положителните оси $x, y, z$.

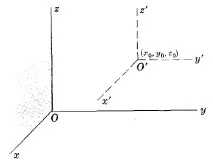
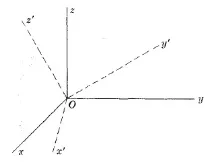
ПРЕОБРАЗУВАНЕ НА КООРДИНАТИ ПРИ ДВИЖЕНИЕ$\left\x=x'+x_0\\ y=y'+y_0\\ z=z'+z_0\end\right.$ $\left\x'=x-x_0\\ y'=y-y_0\\ z'=z-z_0\end\right.$

където $(x, y, z)$ са старите координати [т.е. координати спрямо системата xyz], $(x', y', z')$ - нови координати [спрямо системата $x'y'z'$] и $(x_0,y_0,z_0)$ координати на новия център $O'$ спрямо старата координатна система $xyz$.

ПРЕОБРАЗУВАНЕ НА КООРДИНАТИ ПО ВРЕМЕ НА ВЪРТЕНЕ

където центровете на системите $xyz$ и $x'y'z'$ са в една и съща точка и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ са насочващите косинуси на осите $x', y', z'$ по отношение съответно на осите $x, y, z$.

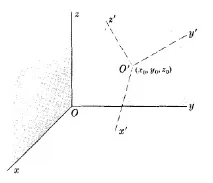
ПРЕОБРАЗУВАНЕ НА КООРДИНАТИ ПО ВРЕМЕ НА ДВИЖЕНИЕ И ВЪРТЕНЕ

$\left\x=l_1x'+l_2y'+l_3z'+x_0\\ y=m_1x'+m_2y'+m_3z'+y_0\\ z=n_1x'+n_2y'+n_3z'+z_0\end\right.$

$ \ ляво \ x '= l_1 (x-x_0)+m_1 (y-y_0)+n_1 (z-z_0) \\ y' = l_2 (x-x_0)+m_2 (y-y_0)+n_2 (z-z_0) \\ z '= l_3 (x-x_0)+m_3 (y-y_0)+n_3 (y-y_0)+n_3 ( Z-Z_0) \ КРАЙ \ НАДЯСНО. $

където $O'$ на системата $x'y'z'$ има координати $(x_0,y_0,z_0)$ по отношение на системата $xyz$ и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ са насочващите косинуси на осите $x', y', z'$ по отношение съответно на осите $x, y, z$.

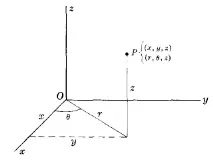
ЦИЛИНДРИЧНИ КООРДИНАТИ $(r, \theta, z)$Точка $P$ може да се дефинира като цилиндрични координати $(r, \theta, z)$, така чеи правоъгълни координати $(x, y, z)$. Трансформацията между тези две координати е

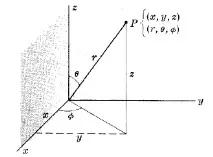
СФЕРИЧНИ КООРДИНАТИ $(r, \theta, \phi)$Точка $P$ може да бъде дефинирана както със сферични координати $(r, \theta, \phi)$, така и с правоъгълни координати $(x, y, z)$. Преобразуването между тези две координати е

$\left\x=r\sin\theta\cos\phi\\ y=r\sin\theta\sin\phi\\ z=r\cos\theta\end\right.$

УРАВНЕНИЕ НА СФЕРА В ПРАВОЪГЪЛНИ КООРДИНАТИ$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$

където сферата има център $(x_0,y_0,z_0)$ и радиус $R$.

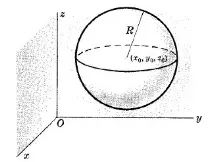
УРАВНЕНИЕ НА СФЕРА В ЦИЛИНДРИЧНИ КООРДИНАТИ$r^2-2r_0r(\theta-\theta_0)+r_0^2+(z-z_0)^2=R^2$

където сферата има център $(r_0;\theta_0;z_0)$ в цилиндрични координати и радиус $R$.

Ако центърът е в началото, уравнението е:

УРАВНЕНИЕ НА СФЕРА В СФЕРИЧНИ КООРДИНАТИ$r^2+r_0^2-2r_0 r\sin\theta\sin\theta_0\cos(\phi-\phi_0)=R^2$

където сферата има център $(r_0; \theta_0; \phi_0)$ в сферични координати и радиус $R$.

Ако центърът е в началото, уравнението е:

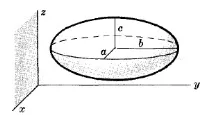
ЕЛИПТИЧЕН ЦИЛИНДЪР С ОС КАТО $z$ ОС$\frac+\frac=1$

където $a, b$ са полуоси на елиптично сечение. Ако $b = a$, фигурата се превръща в цилиндричен цилиндър с радиус $a$.

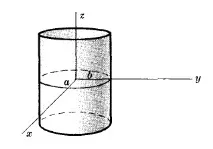
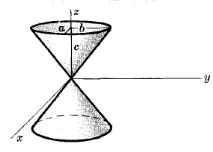
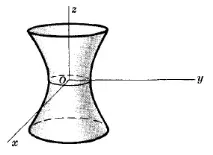
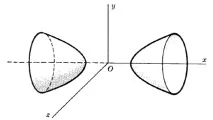
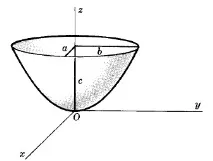
Обърнете внимание на ориентацията на осите на тази фигура.

---