Атомен множител

Интензитетът на лъча, разпръснат от атома, може да се счита за равен на A at = S a e, ако всички електрони са разположени в една точка. Всъщност атомът има краен размер, сравним с дължината на вълната. Следователно вълните, разпръснати от различни части на електронния облак на атома, ще се компенсират частично, т.к. ще се различава във фазата, Фигура 15. Следователно A при S a e . По този начин интензитетът на разсейване в дадена посока е равен на произведението на определен коефициент f 2, наречен атомен фактор, и интензитетът на разсейване от един свободен електрон I e:

Интензитетът на разсейване от един електрон според формулата на Томсън е равен на

Тези. интензитетът на разсейване от атома ще бъде

Фиг.15. Разсейване на рентгенови лъчи от атом с краен размер.

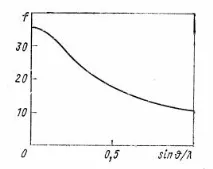
Атомната амплитуда зависи от дължината на вълната, серийния номер на елемента и ъгъла на разсейване, формата на тази зависимост е показана на фигура 1.13. Може да се покаже, че

където u(r) = 4 p r 2 r (r);

r (r) - вероятността за намиране на електрон в обем dV, отдалечен от центъра на атома на разстояние r;

s = f sin Q и f е фазовата разлика на вълните, разпръснати от обема dV по отношение на началото.

Фиг.16. Зависимост на атомния фактор на разсейване от ъгъла и дължината на вълната.

температурен фактор

В решетката атомите вибрират, т.е. не заемат местата, които са предписани в модела на идеална кристална решетка.

Означаваме с D x n изместването на атома спрямо п. В случая, когато честотата на промяна на х е голяма в сравнение с времето на измерване, но малка в сравнение с честотата на рентгеновите лъчи, тогава можем да предположим, че дифракцията възниква върху фиксирани набори от атоми и средният интензитет дава интензитета на всички конфигурации.

---