Балансиращи механизми

Когато връзките на механизма се движат в кинематични двойки, възникват допълнителни динамични натоварвания от силите на инерцията на връзките. Това се дължи на факта, че центровете на масата на връзките в общия случай имат променливи в големината и посоката на ускорение. Тъй като всеки механизъм има фиксирана връзка-стойка, тогава доста определени динамични натоварвания също влияят на стойката на механизма. От своя страна, през стелажа, тези товари се прехвърлят към основата на механизма. Динамичните натоварвания, възникващи по време на движението на механизма, са източници на допълнителни сили на триене в кинематични двойки, вибрации на връзките и основата, допълнителни напрежения в отделни връзки на механизма, причина за шум и др. Следователно при проектирането на механизъм задачата е да се изберат рационално масите на връзките на механизма, което гарантира пълното или частично елиминиране на тези динамични натоварвания. Решението на подобен проблем, свързан с динамичното проектиране на машинен механизъм, се нарича неговото балансиране.

Целта на балансиращите механизми е да елиминират променливите влияния върху основата, които причиняват кинематични вибрации, както на самата основа, така и на сградата, в която се намира.

Концепцията за дисбаланса на механизма (връзка)

Помислете за плосък механизъм (фиг. 10.1), чиято начална връзка 1 се върти с постоянна ъглова скорост. В този случай всички останали връзки ще се движат с ъглови ускорения, а масовите центрове S 1 , S 2 , S 3 ще имат линейни ускорения.

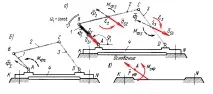
Нека приведем цялата система от инерционни сили в центъра А, в резултат на което цялата тази система ще бъде сведена до общ главен вектор:

и към общия главен момент: , (10.2)

защото 1 = с nst , тогава М Ф1 = 0 .

Динамичните компоненти на базовото натоварване са числено равни на общотоглавния вектор Ф и общия главен момент М Ф на системата от инерционни сили.

Един механизъм се счита за балансиран, ако главният вектор и главният момент на инерционните сили са равни на нула.

Ако общият главен вектор на инерционните сили на механизма Ф 0, тогава такъв механизъм се нарича статично неуравновесен.

Ако М Ф 0, но Ф = 0 - моментен дисбаланс.

Ако М Ф 0 и Ф 0 - динамичен дисбаланс.

Пълното балансиране на лостовите механизми е много трудна задача, поради което в повечето случаи те се ограничават до статичното им балансиране. Въпреки това, не винаги е възможно да се приложи напълно. В тези случаи се извършва частично статично балансиране. При статично балансиране на механизма е необходимо да се осигури следното условие:

Тъй като масата на системата от всички движещи се звена е m i 0 , тогава ускорението на центъра на масата S на тази система трябва да бъде равно на нула (и SM =0). Това условие е изпълнено, когато центърът на масата S на системата от подвижни връзки на механизма не се движи. По този начин статичното балансиране е такова действие, в резултат на което центърът на масата на системата от движещи се връзки на работния механизъм става неподвижен.

На практика статичното балансиране най-често се извършва по три начина:

избор на симетрични схеми на механизми;

Пример за такъв механизъм е двоен коляново-плъзгащ механизъм, използван за мотоциклети и други двигатели с вътрешно горене (фиг. 10. 2).

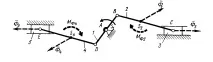
Механизмът е направен наклонен, дясната и лявата биелно-бутална група 2-3 и 4-5 са напълно еднакви, центърът на тежестта S 1 на коляновия вал е върху оста на въртене (F 1 =0). Ф =Ф 1 +Ф 2 +Ф 3 +Ф 4 +Ф 5 = 0, което показва пълната статична уравновесеност на механизма.

Въпреки това, M F =M F2 + M F4 + M A (F 2) + M A (F 4) 0, т.е. Механизмът няма моментен баланс.

монтаж на коригиращи маси (противотежести);

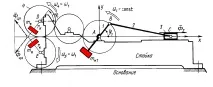
поставяне на противотежести върху допълнителни връзки или кинематични вериги

Най-очевидният и прост метод за балансиране на механизмите е методът за заместване на масите.

Метод на заместващата маса

Когато се използва методът за заместване на масите, връзката на механизма с разпределена маса се заменя с изчислителен модел, който се състои от точкови маси. Референтните точки на масите могат да бъдат избрани произволно, но обикновено резервните маси се намират в пантите.

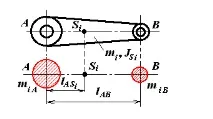
Връзка с разпределена маса:

Модел с резервни маси:

Условия за преход от връзка с разпределена маса към модел

с точкови маси

Запазване на масата на модела и връзката: m iA + m iB = m i ; (10.4)
Запазване на позицията на центъра на масата: l ASi = const ,

m iA l ASi = m iB (l AB l ASi ) (10.5)

Запазване на инерционния момент: . (10.6)

Очевидно е, че е невъзможно да се изпълнят трите условия от система с две маси, следователно, в случай на статично балансиране на механизми, те се ограничават до изпълнението на първите две условия. (За да се гарантира, че и трите условия са изпълнени, трябва да се въведе трета маса m iSi в S i.)

Методът за замяна на масите е следният: всяка връзка на механизма трябва да бъде заменена с две концентрирани маси, след което да се въведат коригиращи маси (противотежести) и да се комбинират със заместващи маси, за да се гарантира, че комбинираните маси в крайна сметка ще бъдат поставени във фиксираните точки на механизма.

Обмислете приложението на метода за заместване на масите за пълно и частично балансиранемеханизми.

Пълно статично балансиране на шарнирната четирираменна връзка

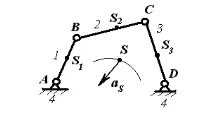
Дадени са: l 1 , l 2 , l 3

l AS1, l BS2, l DS3

m K1, m K3; l K1, l K3

Заменяме всяка връзка с разпределена маса с две концентрирани маси, използвайки системата от уравнения на прехода:

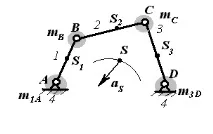
Комбинирайте масите, поставени в точки B и C:

m B = m 1B + m 2B, m C = m 2C + m 3C.

Така даденият механизъм ще бъде заменен от четири маси, концентрирани в точки A , B , C , D . Връзките станаха инертни. Центърът на масата S на системата остана на същото място. По време на работа на механизма центърът на масата S се движи с ускорение a S , което означава, че дадения механизъм е статически неуравновесен.

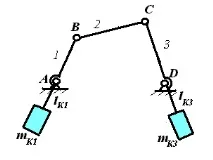
Нека поставим противотежести (коригиращи маси) m К1 , m К2 върху връзки 1 и 3 по такъв начин, че центровете на масата на системите ( m В , m К1 ) и ( m С , m К3 ) да бъдат в точките A и D . За това трябва да бъдат изпълнени следните отношения:

m K1 l K1 = m B l 1; m K3 l K3 = m С l 3 . (10.7)

Масите на противотежестите m K1 и m K3 се определят от съотношения (10.7), ако посочим размерите l K 1 и l K 3 .

Нека докажем, че механизмът е станал статично балансиран, т.е. центърът на масата на системата е неподвижен. Комбинирайте масите, поставени на връзки 1 и 3:

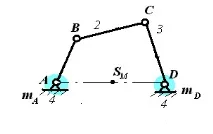
m A \u003d m 1A + m B + m K1;

m D \u003d m 3 D + m C + m K3

Даденият механизъм може да бъде заменен със система от две фиксирани маси m A и m D , така че центърът на масата на тази система и центърът на масата на дадения механизъм, но допълнен с противотежести, също ще станат фиксирани. Това означава, че е постигнато статичното балансиране на дадения механизъм. Центърът на масата на балансиран механизъм е разположен на фиксирана права линия AD = l 4, а разстоянието до центъра на масата можесе намира от отношението:

Масата на целия механизъм m = m 1 + m 2 + m 3 + m K 1 + m K 2.

Пълно статично балансиране на коляно-плъзгащия механизъм

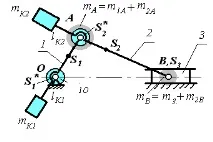
Дадени са: l 1 , l 2 , l OS1 , l AS2 ;

S 3 е същото като T. B.

Заменяме всяка връзка с две концентрирани маси, използвайки системата от уравнения на прехода:

Комбинирайте масите, поставени в точки A и B:

m A \u003d m 1A + m 2A, m B \u003d m 2B + m 3.

Масата m B се балансира от противотежест с масата m K2, определена от връзката: m K 2 l K 2 = m B l 2, (дължината l K 2 е зададена)

Точка А става център на масата на балансираната връзка 2 с масата

m * A \u003d m A + m B + m K2.

Балансира се от коригиращата маса m K1.

След инсталиране на две коригиращи маси, общият център на масата става фиксиран и ще бъде разположен на оста на въртене на манивелата на вала (в точка O). Точка O в този случай е центърът на масата на целия механизъм, т.е. r SM = 0 и m M = m 1 + m 2 + m 3 + m K 1 + m K 2 .

При пълно статично балансиране една от противотежестите е монтирана на свързващия прът (връзка 2), което драстично увеличава размерите и теглото на механизма, следователно се използва частично (непълно) балансиране, постигайки движение на центъра на масата по специална (изчислена) траектория.

Частично статично балансиране, при което центърът на масата се движи по водачите на плъзгача

(балансиране на вертикалната компонента на инерционните сили)

Всяка от връзките се заменя с две концентрирани маси, като се използва системата от уравнения (10.4) и (10.5):

Масите, поставени в пантите A и B, се комбинират:

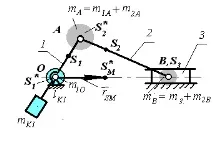
m A \u003d m 1A + m 2A, m B \u003d m 2B + m 3.

Масата m A се балансира от масата на противотежестта m K1

INВ този случай само въртящата се част от заместващите маси е балансирана.

За да намерим траекторията на центъра на масата на частично балансиран механизъм, ние определяме параметрите на радиус вектора на центъра на масата ( r Smin и r S ):

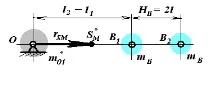
\u003d m K1 + m 1O + m 2A + m 1A;

Това балансиране се използва за коляно-плъзгащи механизми с вертикален плъзгач или с хоризонтален плъзгач с ниска основа.

Частично балансиране за случая, когато центърът на масата се движи по дъга, чиято хорда е перпендикулярна на оста на водача на плъзгача

Всяка връзка се заменя с две концентрирани маси, като се използва системата от уравнения (10.4) и (10.5):

Масите, поставени в точки A и B, се комбинират:

m A \u003d m 1A + m 2A, m B \u003d m 2B + m 3.

Този механизъм се балансира от коригиращата маса m K1:

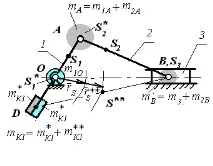
Коригиращата маса балансира масата m A : .

Коригиращата маса балансира масата m B . Стойността му се намира от условието, че центърът на масата и m A се намира в t.O. Центърът на масата и m B лежи на линията BD и я разделя по отношение на x / y, т.е. x \u003d m B y. През сегмента OS ** начертаваме права линия, успоредна на AB и след това от подобието на триъгълници намираме:

Обща коригираща маса |

Радиус-векторът на центъра на масата се намира от отношенията:

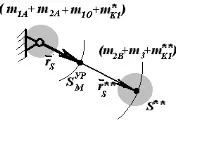
където m \u003d m 3 + m 1 + m 2 + m K1;

Това балансиране се използва за машини, монтирани на висока основа.