Басрефлексна зона
Това, което може да изглежда просто на пръв поглед, някои хора разбират погрешно. Как например да направите кръгъл фазоинвертор със същата площ, но правоъгълен, квадратен, триъгълен и т.н.? Започваш да помниш геометрията.
Запасете се с лист и химикал, тъй като ще направя изчислението ръчно, но никой не забранява използването на онлайн калкулатор за тези изчисления (напримертук ). Изчисляването на различни области също ще продължи от предварително известната площ на кръглия фазов инвертор (тръба). Точните размери ще трябва да изберете сами според вашия район. Например ще избера различни области от фазоинвертор с диаметър 10 см.
Кръгова област
Площ на кръг:S = ∏ ∙ r 2
Пример: S \u003d 3,14 ∙ 5 2 \u003d 78,5 cm 2
Полукръг
Площ на полукръг:S = (∏ ∙ r 2 ) / 2
Намерете радиуса на окръжността по отношение на площта:r= √ (S/ ∏)
Пример: r = √ (78,5 / 3,14) = 5 cm
Проверяваме: S \u003d 3,14 ∙ 5 2 \u003d 78,5 cm 2
Прорезен (правоъгълен или квадратен) фазов инвертор
Площ на правоъгълник (квадрат):S = a ∙ b
За прорезен фазов инвертор ще взема съотношение на страните от около 1 към 12.
Оказва се: S \u003d 2,5 ∙ 31,4 \u003d 78,5 cm 2
Диамант
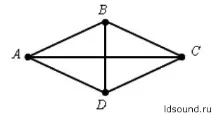
Диамантена площ:S = (AC∙BD) / 2
Изчислете друг диагонал BD през площ и диагонал AC:BD = 2 ∙S/AC
Пример: нека дадем AC диагонали 15 cm, тогава BD = 2 ∙ 78,5 / 15 ≈ 10,4666 cm
Проверяваме: S \u003d 15 ∙ 10.4666 / 2 \u003d 78.4995 cm 2
Триъгълник
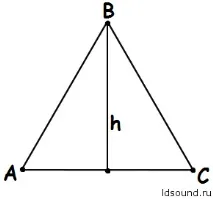
Площ на триъгълника:S= ½ ∙AC∙h (половината от произведението на дължината на една страна на триъгълник и дължината на височината, начертана към тази страна). Триъгълникът може да бъде както правилен, така и грешен, но правилният е по-лесен за броене и изграждане. Въпреки че за неправилен триъгълник тази формула също е уместна.
Ако нашият триъгълник е правилен (всички страни са равни една на друга и всички ъгли са равни на 60 °), нека височината h = 11 cm, тогава всяка от страните, но в този случай AC, ще бъде:AC = 2S/h
Пример: AC = 2 ∙ 78,5 / 11 = 14,2727 cm
Проверяваме: S \u003d ½ ∙ 14.2727 ∙ 11 \u003d 78.4998 cm 2
Трапец
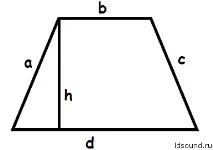
Площ на равнобедрен трапец:S = ((b+d) / 2) ∙h
Пример: Нека наместим трапец през известната ни площ, дадена височина и горна страна. Нека h, височината на моя трапец, е 3 см, а страната b = 20 см, тогава основата:
Успоредник
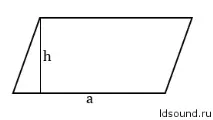
Площ на паралелограма:S=ah
Пример: нека височината е 3 cm, тогава страната a \u003d 78,5: 3 ≈ 26,17 cm
Проверяваме: S \u003d 3 ∙ 26,17 \u003d 78,51 cm 2
Правилен петоъгълник
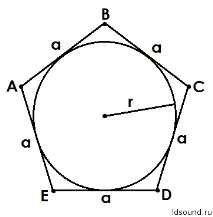
Площ на правилен петоъгълник:S =r∙n∙a/2, където
n – брой страни;
r – радиус на вписаната окръжност;
a е една от страните на петоъгълника.
С петоъгълник вече е по-трудно да изберете областта ръчно, тъй като от известните стойности имаме само броя на страните n. Затова препоръчвам да използвате онлайн калкулатор. Направо ще кажа, че в моята версия, страна a \u003d 6,64 cm, с тази стойност площта е 75,85 cm 2.
Правилен шестоъгълник
Същото с шестоъгълникаи с петоъгълник, така че няма да анализирам сложни изчисления - онлайн калкулатор за помощ.
Елипса
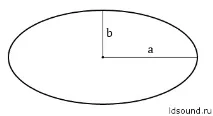
Площта на елипсата е равна на произведението на ∏ от голямата полуос и малката полуос:S=∏ab
Голямата полуосa трябва да бъде точно два пъти по-голяма от малката полуосb. Ако някой иска да изчисли ръчно, моля, използвайте моя пример по-долу.
Пример: изборът на площ ще стане чрез известно число ∏ и необходимата площ, в моя случай 78,5 cm 2.
78,5 \u003d 3,14 ∙ 2x ∙ x
x 2 \u003d 78,5: 6,28 \u003d 12,5
Проверяваме: 3,14 ∙ 3,53 ∙ 7,06 \u003d 78,25 cm 2
В заключение. Няма да давам площта на такива фигури като звезда или кълчища, това е твърде голямо извращение. Но никой не забранява да разделите звезда на 5 триъгълника и един петоъгълник и по някакъв начин да изчислите всичко това.
Също така не забравяйте, че има и фазови инвертори с разширение навън. Такива форми ви позволяват да премахнете "свирката" в тръбата и да намалите нейната дължина. Но моят пример не се отнася за това.
От моя собствен опит ще кажа, че тръбата е по-лесна за производство и понякога е налична, но по отношение на свирката и сложността на производството бих използвал прорезен (правоъгълен) фазов инвертор.