Борба с мелниците
В тази статия лирическият герой оспорва оптималното прилагане на класическия полином на Лагранж (Фароу) интерполатор, по време на битката той случайно открива и доказва тривиално математическо заклинание, от което никого не се нуждае, с което се опитва да изтласка врага, но според резултатите от всички рундове на битката, равенството е фиксирано с решение на съдиите.
Къде виждате великани? — попита Санчо Панса. „Да, ето ги, с огромни ръце“, отговори господарят му. „Някои от тях имат ръце, дълги почти две мили. - Извинете, сеньор - възрази Санчо, - това, което виждате там, изобщо не са великани, а вятърни мелници; това, което приемате за ръцете им, са крила: те се въртят във вятъра и задвижват воденичните камъни. - Сега можете да видите неопитен авантюрист - каза Дон Кихот - това са великани. И ако се страхувате, тогава се отдръпнете и се молете, а междувременно аз ще вляза в жестока и неравна битка с тях ...
Един ден мой приятел ме помоли да моделирам за него проста и евтина версия на повторно семплиране (промяна на честотата на семплиране) на цифров сигнал. Нямаше специални изисквания за линейността на честотната характеристика и фазовата характеристика и имаше желание да се спести време и памет, така че някои методи като полифазни интерполиращи банки на FIR филтри бяха незабавно изключени от разглеждане и основното внимание беше обърнато на методите за локална полиномна интерполация. Полиномите се изчисляват бързо и лесно, техните коефициенти изискват малко памет за съхранение и с един набор от коефициенти можете да изчислите всякакви стойности в рамките на първоначалния интервал на вземане на проби.
Запознайте се с врага - изпълнение на Farrow
Известно е, че през всякакви N точки (следователно и по-нататък, за определеност, ниеще разгледаме еднаква решетка - със същата стъпка, въпреки че това не е предпоставка за много от описаните техники и методи), и така през всякакви N точки с различни абсцисни координати можете да начертаете един полином от N-1 ред, уникално определен от набор от N коефициенти (прочетох, че LaTex на Хабре не е директно, а чрез картини, които са тежки и краткотрайни, така че ще използвам само горни и долни индекси в html таговете):
За удобство на изчисленията нормализираме нашата унифицирана аргументна мрежа до цели числа, като използваме четири точки като пример, избираме удобен аргументен интервал (Фароу избра от [-2, 1] с централен интервал от [-1, 0]) и записваме система от линейни уравнения от условието на полинома, минаващ през нашите 4 точки:
Можете да го решите както искате, дори ако обърнете матрицата с Гаус, но Фароу оптимизира броя на операциите за изчисляване на коефициентите на този полином:
Общо операции:
- 1 умножение по константа (1/6)
- 2 делено на 2 (бързо както при цяло число, така и при аритметика с плаваща запетая)
- 8 събиране/изваждане
Първи претендент - Catmull-Roma Spline
Може да се види, че както желаният полином, така и всички негови производни са линейни комбинации от неизвестниполиномни коефициенти. Следователно можем да зададем условията за равенство на производните от всякакъв ред във възлите на мрежата на дадени стойности и да получим линейна система от уравнения за коефициентите на полинома. Локалният кубичен сплайн на Hermite е конструиран според четири условия: стойностите на полинома и неговата първа производна в краищата на интервала. И можем да получим приблизителните стойности на тези производни в необходимите точки, като диференцираме интерполиращия полином на Лагранж, минаващ през тях. Например нормализираме аргументите на четири точки към интервала [-1, 2], вземаме три точки с аргументи, начертаваме парабола през тях и изчисляваме нейните коефициенти. И тъй като се нуждаем само от стойността на първата производна на тази парабола в централната точка 0, достатъчно е да изчислим нейния коефициент на първата степен на аргумента и той ще бъде използван като производна за конструиране на сплайн. Производната на дясната граница на интервала се изчислява по подобен начин. В резултат на просто изчисление получаваме следната система от уравнения за коефициентите на сплайн:
чието решение може да се получи в следната форма:
Можем да забележим, че по време на последователна (поточно) обработка на входните данни, производната на лявата граница на интервала е същата като производната на дясната граница на предишния интервал, което означава, че на всеки интервал трябва да изчислим само една производна - в дясната граница на интервала, и да вземем стойността в лявата от тази, съхранена в предишното изчисление в дясната. С помощта на такива спестявания на съвпадения получаваме следния брой операции за изчисляване на коефициентите на полинома:
- 2 умножение/деление на 2
- 7 събиране/изваждане
Вторият претендент е 6-точковият сплайн на Hermite
Ако щемза да оцените производните в краищата на централния интервал не с три, а с пет точки, тогава изчислението им ще стане малко по-сложно, но останалите формули няма да се променят:
Като се вземе предвид предишната забележка за необходимостта да се изчисли само една производна на всеки интервал, броят на операциите:
- 1 умножение по константа (2/3)
- 2 умножения/деления на степен 2
- 9 събиране/изваждане
Сравнение на опциите
По отношение на броя на операциите сплайнът Catmull-Roma значително превъзхожда Farrow, Hermit губи малко в 6 точки (с едно добавяне). Също така си струва да се отбележи, че и двата сплайна имат първи ред на гладкост (непрекъсната нула и първи производни) поради тяхната конструкция, за разлика от Фароу, който не гарантира непрекъснатостта на производната. Но остава въпросът за точността на апроксимацията на функциите чрез тези сплайнове. Синусът беше избран като тестова функция и беше апроксимиран от горните варианти на сплайни за различно разстояние на мрежата, което се нормализира към относителната стойност на броя точки за период. Измерена е стойността на максималното отклонение от апроксимираната функция. Резултатите са представени на графика, при избор на логаритмична скала по двете оси, зависимостите са почти линейни, сближаващи се в една точка, когато честотата на дискретизация намалява и се доближава до честотата на Найкуист (2 точки на период от апроксимирания тестов синус).
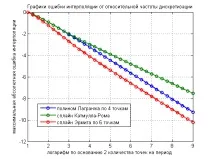
Графиката показва, че сплайнът Catmull-Roma е по-нисък от Farrow по отношение на точността, а последният е по-нисък от Hermite в 6 точки, с почти същия брой операции, необходими за изчисляване. Не беше възможно да се спечели чиста победа, но по принцип резултатът не е лош IMHO.
Заклинание
Можем да развием общата идея за сплайн на Ермит в производни на всекипоръчки. Например, нека изградим сплайн според следните условия: неговите стойности в краищата на интервала съвпадат със стойностите на показанията в тези точки, авторитепроизводни в тези точки съвпадат с техните оценки, направени от параболи чрез тройки от точки - тоест всичко е като в Catmull-Rom, само вместо първото ще вземем вторите производни - парабола, като полином от втори ред ial, напълно ще ни позволи да ги изчислим. И тук с изненада установяваме, че така построеният сплайн напълно съвпада с уважаемия ни Фароу, който всъщност е полиномът на Лагранж. Който желае, може да го провери, дори ще напиша формула за оценка на втората производна на парабола по 3 точки (въпреки че това е тривиално упражнение):
Щастлив мач? Случайно, защото има малко точки и редът на полинома е малък? Чрез числена проверка на този факт върху различен брой точки и реда на полиномите, се убедих, че заклинанието работи:
Нека имаме интерполационен полином, конструиран от някои стойности върху четен брой точки от еднаква решетка
Тогава всички четни производни на този полином в точката x0 съвпадат с производните на същите порядъци на интерполационния полином, конструиран от точките
и в точката x1, полиномът, конструиран от точките
Доказателство. Да разгледаме функция върху равномерна решетка с нечетен брой точки - ще направим преместване на аргумента, което довежда аргумента на централния възел до 0
Има единственият интерполационен полином P0(x). Нека добавим още едно xk+1 към този набор от точки (няма значение за доказателството дали ще го добавим вдясно, вляво или дори в средата, а не към възлите на оригиналната мрежа). Интерполационният полином върху разширен набор от точки при условие на равномерна мрежа може да бъде представен във формата на Нютон
където А е някаква константа.Наистина, тази добавка добавка трябва да има нулеви стойности в точките на първоначалния полином, а константата A се определя от условието за равенство P1(xk+1) = yk+1, необходимата стойност на полинома в добавената точка. Поради еднородността на мрежата -x-i = xi, тогава
Очевидно дясната страна съдържа сумата от P0(x) и полином с ненулеви коефициенти само за нечетни степени на аргумента. Следователно коефициентите при четни степени на полиномите P1(x) и P0(x) съвпадат и всички четни производни на всеки полином при нула се определят само от съответния му коефициент при четна степен на аргумента. Така всички четни производни на P1(x) и P0(x) съвпадат. Горното разсъждение е валидно за всяко местоположение на добавената точка xk+1, по-специално, когато я добавяте отдясно или отляво на оригиналната мрежа. По този начин производните на четните порядъци при нула за оригиналния полином и полинома по отношение на разширеното множество от точки съвпадат. ч.т.д.
Последен кръг - Лагранж по Фароу с Лагранж по производни
Тъй като интерполационният полином от минималния ред е уникален, тогава, като вземем предвид току-що доказаното заклинание, можем да го изградим чрез условия върху стойностите на четните производни в краищата на централния интервал - например полином от 5-ти ред през 6 точки според 6 условия: стойности на проби и втори и четвърти производни, изчислени за всеки пет точки. В този случай използвайте същата оптимизация, описана по-горе - изчисляване на производни само в дясната граница на всеки интервал. В първоначалната формулировка на полинома, минаващ през всички точки, тези инварианти не бяха очевидни. Нека приложим това към нашия оригинален 4-точков Лагранж и оптимизираме броя на операциите. Веднага ще дам Matlab кода на моята версия, както и версията на участника с никнейм _Anatoliy от форумаелектроника, която независимо и независимо победи Фароу дори преди моите експерименти:
Както можете да видите, и двата кода съдържат по-малко операции за изчисляване на коефициентите на полинома, така че по отношение на спорта, мисля, че и двамата спечелихме. И въпреки че има мнения, че това е спестяване на съвпадения, че в наше време, когато космическите кораби плуват навсякъде, има математически копроцесори с интегрирани операции с числа с плаваща запетая, скоростта на операциите е сравнима със скоростта на преместване на съдържанието на регистрите и още повече четене / запис на памет за запазване / възстановяване на изчислени стойности - такива оптимизации не дават нищо, все още имам известно чувство на удовлетворение от резултатите, въпреки слабата им практическа значимост ант.
И тук можете да получите грант за тестов период на Yandex.Cloud. Необходимо е само да въведете "Habr" в полето "секретна парола".