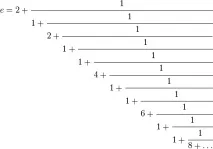
Числото на Ойлер е

Играе важна роля в диференциалното и интегралното смятане, както и в много други клонове на математиката.

2.718 281 828 459 045 235 360 287 471 352 662 497 757… [1]

Съдържание

Методи за определяне

Числотоeможе да се дефинира по няколко начина.

• През границата: (втора забележителна граница).
• Като сбор от серията: или .
• Като едно числоaза което
• Като единственото положително числоa, за което

• Това свойство играе важна роля при решаването на диференциални уравнения. Например, единственото решение на диференциално уравнение е функцията , къдетоcе произволна константа.
• Числотоeе ирационално и дори трансцендентално. Това е първото число, което не е специално изведено като трансцендентно, неговата трансцендентност е доказана едва през 1873 г. от Чарлз Ермит. Приема се, чеeе нормално число, т.е. вероятността за появата на различни цифри в записа му е еднаква.
• , вижте по-специално формулата на Ойлер

Друга формула, свързваща числатаеиπ, т.нар. "интеграл на Поасон" или "интеграл на Гаус"

За всяко комплексно числоzса верни следните равенства:

Числотоeсе разширява в безкрайна продължителна дроб, както следва: , т.е.

Представяне на каталонски:

Същата константа е изчислена за първи път от швейцарския математик Бернули при анализиране на следната граница:

Първата известна употреба на тази константа, където тя е обозначена с букватаb, се среща в писма от Лайбниц до Хюйгенс, 1690-1691.

Букватаeзапочва да се използва от Ойлер през 1727 г. ипървата публикация с това писмо е неговият труд „Механиката или науката за движението, формулирана аналитично“ през 1736 г. Съответноeобикновено се наричачисло на Ойлер. Въпреки че някои по-късни учени са използвали букватаc, букватаeе използвана по-често и днес е стандартната нотация.

Защо е избрана букватаeне е точно известно. Може би това се дължи на факта, че думатаexponential(„експоненциален“, „експоненциален“) започва с него. Друго предположение е, че буквитеa,b,cиdвече са били доста широко използвани за други цели, аeе първата "свободна" буква. Неправдоподобно е Ойлер да е избралeкато първа буква от фамилното си име (на немскиEuler).

Методи за запаметяване

Доказателство за ирационалност

Нека е рационално. Тогава , където и са положителни числа, откъдето

Умножавайки двете страни на уравнението по , получаваме

Преминаване към лявата страна:

Всички членове от дясната страна са цели числа, следователно:

- цяло

Но по друг начин

Интересни факти

• IPO на компанията през 2004 г. обяви намерението на компанията да увеличи приходите си с $2,718,281,828. Заявената цифра е първите 10 цифри на известна математическа константа.
• В езиците за програмиране знакътeв експоненциална нотация за числови литерали съответства на числото 10, а не на числото на Ойлер. Това се дължи на историята на създаването и използването на езика за математически изчисления FORTRAN[2] :

Започнах да програмирам през 1960 г. във FORTRAN II, използвайки компютър IBM 1620. По това време, през 60-те и 70-те години, FORTRAN използваше само главни букви. Може би това се е случило, защотоповечето от по-старите входни устройства бяха телетипи, които работеха с 5-битов код на Бодо, който не поддържаше малки букви. Буквата E в експоненциалната нотация също беше главна и не беше смесена с основата на естествения логаритъмe, който винаги се пише с малки букви. Символът E просто изразяваше експоненциалния характер, т.е. обозначаваше основата на системата - обикновено беше 10. В онези години програмистите широко използваха осмичната система. И въпреки че не го забелязах, ако видях осмично число в експоненциална форма, бих предположил, че означава основа 8. Първият път, когато срещнах използването на малкоeв експоненциална нотация в края на 70-те, беше много неудобно. Проблемите се появиха по-късно, когато малките букви се преместиха във FORTRAN по инерция. Имахме всички необходими функции за работа с естествени логаритми, но всички те бяха написани с главни букви.

---