Цифрови и азбучни изрази
Записите за действие се наричат числови изрази.
Числото, получено в резултат на извършването на всички тези действия, се нарича стойност на израза.
Израз, съдържащ букви, се нарича буквален израз.
Числата, които заместват буква, се наричат стойности на тази буква.
Уравнение
Уравнение е равенство, съдържащо буква, чиято стойност трябва да се намери.
Стойността на буквата, при която се получава правилно числово равенство, се наричакорен на уравнението.
За да решите уравнение означава да намерите всичките му корени или да се уверите, че няма. За да намеритенеизвестния член, извадете известния член от сумата:
За да намеритенеизвестното умаляемо, добавете субтрахентая и разликата:
За да намеритенеизвестен субтрахен, извадете разликата от умаляваното:
Умножение и деление на естествени числа
Умножение на естествени числа и неговите свойства
Умножете число mпо естествено число n - означава да намеритесума n
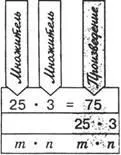
членове, всеки от които е равен на m.
Изразът m n и стойността на този израз се наричат
продукт числа. Числата се наричатмножители.
Свойства на умножението:
1.Комутативно свойство на умножението : Продуктът на две числа не се променя, когато факторите се пренаредят:a b = b a
2.Асоциативно свойство на умножението : За да умножите число по произведението на две числа, можете първо да го умножите по първия множител и след това да умножите получения продукт по втория множител:a (b c) = (a b) c.
3.Свойството за умножение по едно : Сумата от членовете, всеки от които е равен на 1, е равна на n:1 · n = n.
4.Собственостумножение по нула : Сборът от членовете, всеки от които е равен на нула, е равен на нула:0 · n = 0.
Знакът за умножение може да бъде пропуснат: 8 x \u003d 8x, или a b \u003d ab, или a (b + c) \u003d a (b + c)
Разделение
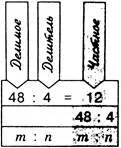
Действието, чрез което продуктът и един от множителите намират друг множител, се нарича деление.
Числото, което се дели, се нарича делимо; числото, на което се дели, се нарича делител, а резултатът от делението се нарича частно.
Коефициентът показва колко пъти дивидентът е по-голям от делителя.
Не можете да делите на нула! Свойства на разделението:
1. При деление на което и да е число на 1 се получава същото число: a: 1 = a.
2. При разделяне на число на същото число се получава единица: a: a = 1.
3. Когато нулата се раздели на число, се получава нула: 0: a = 0.
За да намеримнеизвестен множител, трябва да разделим продукта на друг множител.
За да намеритенеизвестен дивидент, трябва да умножите частното по делителя.
За да намеритенеизвестен делител, разделете дивидента на частното. 48 : х = 4
Деление с остатък
Остатъкът винаги е по-малък от делителя.
3
Тук числото 23 е дивидентът, 4 е делителят, 5 е частичното частно и 3 е остатъкът.
Ако остатъкът е нула, тогава казват, че дивидентът се дели на делителябез остатък или в противен случайнапълно.
За да намерите дивидент a при деление с остатък, трябва да умножитенепълното частноc поделителяb и да добавите остатъка d към получения продукт.
a = c b + d
Опростяване на изрази
Свойства на умножението:
1.Разпределително свойство на умножението по отношение на събирането :To
умножете сбора по числото, можете да умножите всеки член по това число идобавете получените продукти:(a + b) c \u003d ac + bc.
2. Разпределително свойство на умножението по отношение на изваждането : До
умножете разликата по числото, можете да умножите числото, което трябва да се намали и извади по това число и да извадите втория от първия продукт:(a - b) c \u003d ac - bc.
3a + 7a = (3 + 7)a = 10a
3y + 7y + 25 = 85 (3 + 7)y + 25 = 85 10y + 25 = 85 10y = 85 - 25 10y = 60