Да овладеят методите за алгоритмизиране и програмиране на формата на представяне на интерполационния полином

Описание: ЦЕЛ НА РАБОТАТА Да се овладеят методите за алгоритмизиране и програмиране на формата на представяне на интерполационния полином на Лагранж с равномерно разположение на възлите. Изучете свойствата на интерполационния полином на Лагранж. Изследвайте зависимостта на грешката на интерполацията на функцията от броя и местоположението на възлите за интерполационния полином на Лагранж.

Дата на добавяне: 2014-06-16

Размер на файла: 265.87 KB

Работата е изтеглена от: 12 души.

Ако тази работа не ви подхожда, има списък с подобни произведения в долната част на страницата. Можете също да използвате бутона за търсене

Министерство на образованието и науката на Украйна

Севастополски национален технически университет

Катедра по техническа кибернетика

Лабораторен доклад

"ИНТЕРПОЛАЦИЯ НА ФУНКЦИИ ПО ПОЛИНОМИ"

студент от група А-22г

Изкуство. учител Алчаков В.В.

Овладейте методите за алгоритмизиране и програмиране на формата на представяне на интерполационния полином на Лагранж с равномерно разположение на възлите.
Изучете свойствата на интерполационния полином на Лагранж.
Изследвайте зависимостта на грешката на интерполацията на функцията от броя и местоположението на възлите за интерполационния полином на Лагранж.

2 ТЕОРЕТИЧНО КРАТКО

Интерполацията е приблизително определяне на стойностите на функцията f ( x ) в междинни точки на даден затворен интервал x B  x  x E на промяната в неговия аргумент x според известните стойности f ( x 1 ), f ( x 2 ),…, f ( x m ). Стойностите на аргумента x i  [ x B , x E ] , i =1,2…, m на интерполираната функция f ( x ) се наричат интерполационни възли.

Интерполацияфункция f ( x ) чрез полином означава изграждането на такъв полином с минимална степен F m ( x ), който удовлетворява следните условия при m интерполационни възли:

f (k) (x i ) = F m (k) (x i ) , i = 1,2,…,m , k = 0,1,…,m i -1 .

Тук f ( k ) ( x i ) са известните стойности на функцията f ( x ) и нейните производни от k -ти ред f ( k ) ( x ) в интерполационните възли, а m i е множествеността на i -тия възел. Ако m i =1, i -тият възел се нарича прост.

Интерполация на функции f ( x ) чрез полином с прости възли ( m i =1, i =1,2,…, m ) означава конструирането на такъв полином с минимална степен F m ( x ), който удовлетворява следните условия при m интерполационни възли:

f ( x i ) = F m ( x i ), i = 1,2,…, m .

Интерполационният полином на Нютон може да бъде представен като

F m ( x ) = , където ,  i ( x ,0)=1.

Интерполационната грешка на функция f(x) за даден интервал обикновено се оценява като максималната стойност за този интервал на абсолютната величина на грешката. Тъй като е невъзможно да се изчисли E ( x ) във всички точки на интервала, статията предлага да се изчисли стойността му в точки

z i = ( i -1) 0,01, i = 1,2,…,101

и дефинирайте оценката на грешката на интерполацията на функцията на дадения интервал [0,1] като e = E ( z i ).

3 ПОСТАНОВКА НА ПРОБЛЕМА

за които е необходимо да се конструира интерполационен полином F m ( x ) във формата на Лагранж

4 ПРОГРАМА СХЕМА НА РАБОТА

5 ПРОГРАМЕН ТЕКСТ

const двойно c1=0;

const двойно c2=0,5;

const двойно c3=0,4;

const двойно c4=-2.47;

const двойно c5=1,46;

двойно f(двойно x)

printf("Въведете броя на интерполационните възли \n");

двойно Q[m];//масив от коефициенти

двоен t[m];//масив от интерполационни възли

printf(" Възел Точна стойност Стойностполиномна грешка\n");

//изчисляване и съхраняване в масива от стойности на коефициентите на интерполационния полином Fm(x);

for(j=1;j Coeff 2 f - ly 5

Q[i]=f(t[i])/Wi; // фактор 1 f - ly 5

//изчисление в цикъл с Zi=(i-1) 0.01, i = 1,2,…,101 функционални стойности, полиномна и интерполационна грешка

for(j=1;j Coeff 2 f - ly 5

//Таблица на позиция 3.1 съгл. стойност на аргумента, извежда 20 стойности (k-1)*0,05

if ((k-1)%5==0) printf("i=%lf F(i)=%lf Fm(Zi)=%lf E=%lf \n",Z,f(Z),x,e);

printf("Прогнозна грешка на интервал=%lf,на възел %lf\n",emax,uz);

6 РЕЗУЛТАТИ НА ПРОГРАМАТА

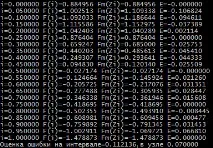
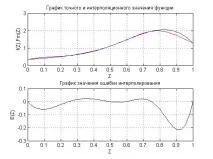
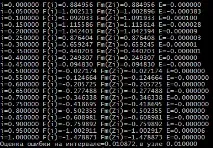
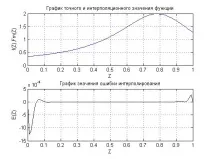
Графики на функцията f ( x ), както и графика на полинома F m ( x ) Представена е и графика на изменението на грешката

Изследван е методът за алгоритмизиране и програмиране на представянето на интерполационния полином на Нютон с равномерно разположение на интерполационните възли, изследвана е зависимостта на интерполационната грешка от броя на възлите m. C остави програма, която реализира интерполацията на полиномиални функции по метода на Лагранж. Правят се следните изводи:

- за постигане на зададената точност на изчисленията на интервала [0,1] са необходими 20 интерполационни възела;

- имайки възможност за подробен анализ на грешката на метода (тъй като първоначалната функция е дадена за изчисляване на точните стойности), бяха съставени графики на грешката на метода за различни m (брой възли), от които следва:

1) най-малката грешка се постига в интервалните точки, които са най-близо до интерполационните възли; грешката нараства приближавайки средата на интервала между възлите;

2) най-голямата грешкасе наблюдават на интервалите между възлите, лежащи на „ръбовете“ на интерполационния интервал [0,1].